Which one is easier to turn— a log or a bench of equal weight and length ? The two have the same coefficient of friction with the ground. Explain.
To determine which object is easier to turn between a log and a bench of equal weight and length, we need to analyze the rotational dynamics of both objects. The key factors to consider are the distribution of mass and the moment of inertia of each object.
1. Identify the Objects: We have two objects: a log and a bench. Both have the same weight (W) and length (L).
2. Understand the Moment of Inertia: The moment of inertia (I) is a measure of an object's resistance to changes in its rotation. It depends on how the mass is distributed relative to the axis of rotation. For a uniform log (cylinder) and a bench (which can be approximated as a rectangular prism), the moments of inertia are different.
3. Calculate the Moment of Inertia:
- For a solid cylinder (log), the moment of inertia about its central axis is given by:
Ilog=12mR2
where m is the mass and R is the radius of the log.
- For a rectangular prism (bench), the moment of inertia about an axis through its center and perpendicular to its length is given by:
Ibench=112mL2
4. Compare the Moments of Inertia: Since both objects have the same weight and length, we can analyze their moments of inertia based on their shapes.
- The log, being cylindrical, has its mass distributed more evenly around its central axis, resulting in a lower moment of inertia compared to the bench.
- The bench, being rectangular, has its mass distributed farther from the axis of rotation, leading to a higher moment of inertia.
5. Conclusion: Since the log has a lower moment of inertia than the bench, it will be easier to turn. Therefore, the log is easier to rotate compared to the bench of equal weight and length.
Final Answer:
The log is easier to turn than the bench of equal weight and length due to its lower moment of inertia.
- For a solid cylinder (log), the moment of inertia about its central axis is given by:
Ilog=12mR2
where m is the mass and R is the radius of the log.
- For a rectangular prism (bench), the moment of inertia about an axis through its center and perpendicular to its length is given by:
Ibench=112mL2
- The log, being cylindrical, has its mass distributed more evenly around its central axis, resulting in a lower moment of inertia compared to the bench.
- The bench, being rectangular, has its mass distributed farther from the axis of rotation, leading to a higher moment of inertia.
The log is easier to turn than the bench of equal weight and length due to its lower moment of inertia.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE353videos
System of particles & rotational Motion
- BOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice90videos
ROTATIONAL MOTION
- BOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise449videos
Thermal Properties of Matter
Similar Questions
A block of mass m slides from the top of an inclined plane of angle of inclination θ & length l. The coefficient of friction between the plane and the block is μ. Then it is observed over a distance d along the horizontal surface having the same coefficient of friction μ, before it comes to a stop. Find the value of d.
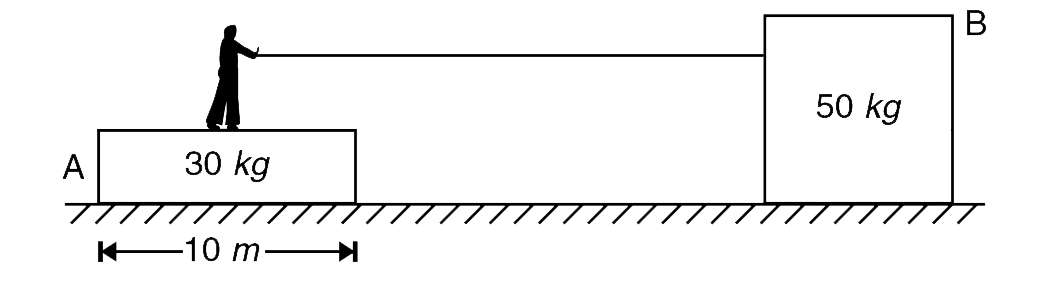
View SolutionA 50 kg man is standing at the centre of a 30 kg platform A. Length of the platform is 10 m and coefficient of friction between the platform and the horizontal ground is 0.2. Man is holding one end of a light rope which is connected to a 50 kg box B. The coefficient of friction between the box and the ground is 0.5. The man pulls the rope so as to slowly move the box and ensuring that he himself does not move relative to the ground. If the shoes of the man does not slip on the platform, calculate how much time it will take for the man to fall off the platform. Assume that rope remains horizontal, and coefficient of friction between shoes and the platform is 0.6.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A spring is compressed between two toy carts to masses m1 and m2. When the toy carts are released, the spring exerts on each toy cart equal and opposite forces for the same small time t. If the coefficients of friction μ between the ground and the toy carts are equal, then the magnitude of displacements of the toy carts are in the ratio
A(a) S1S2=m2m1B(b) S1S2=m1m2C(c) S1S2=(m2m1)2D(d) S1S2=(m1m2)2 - Question 2 - Select One
Which one of the following gives the dimensional formula of coefficient of friction?
A[MLT−2]B[M2LT−2]C[M0L0T0]D[M2LT] - Question 3 - Select One
A uniform - ladder of length 70 m and weight W rests against a vertical wall at an angle of 45∘ with the wall. The coefficient of friction of the ladder with the ground and the wall are 12 and 13 respectively. A man of weight W/2 climbs the ladder without slipping. The height in metres to which he can climb is
A30B40C50D60
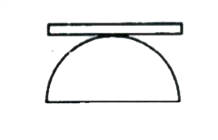
A board is balanced on a rough horizontal semicircular log. Equilibrium is obtained with the help of addition of a weight to one of the ends of the board when the board makes an angle θwith the horizontal. Coefficient of friction between the log and the board is
 View Solution
View SolutionWhich of the following sets of compounds have their molecular weight and equivalent weight the same?
View SolutionWhich of the following sets of compounds.have their molecular weight and equivalent weight the same?
View SolutionTwo objects losing the same weight when immersed in water must have the same
View SolutionTwo blocks of mass 2m and m slide down the slope AB having same friction coefficient Then:
 View Solution
View Solution

