Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
Video Solution
Text Solution
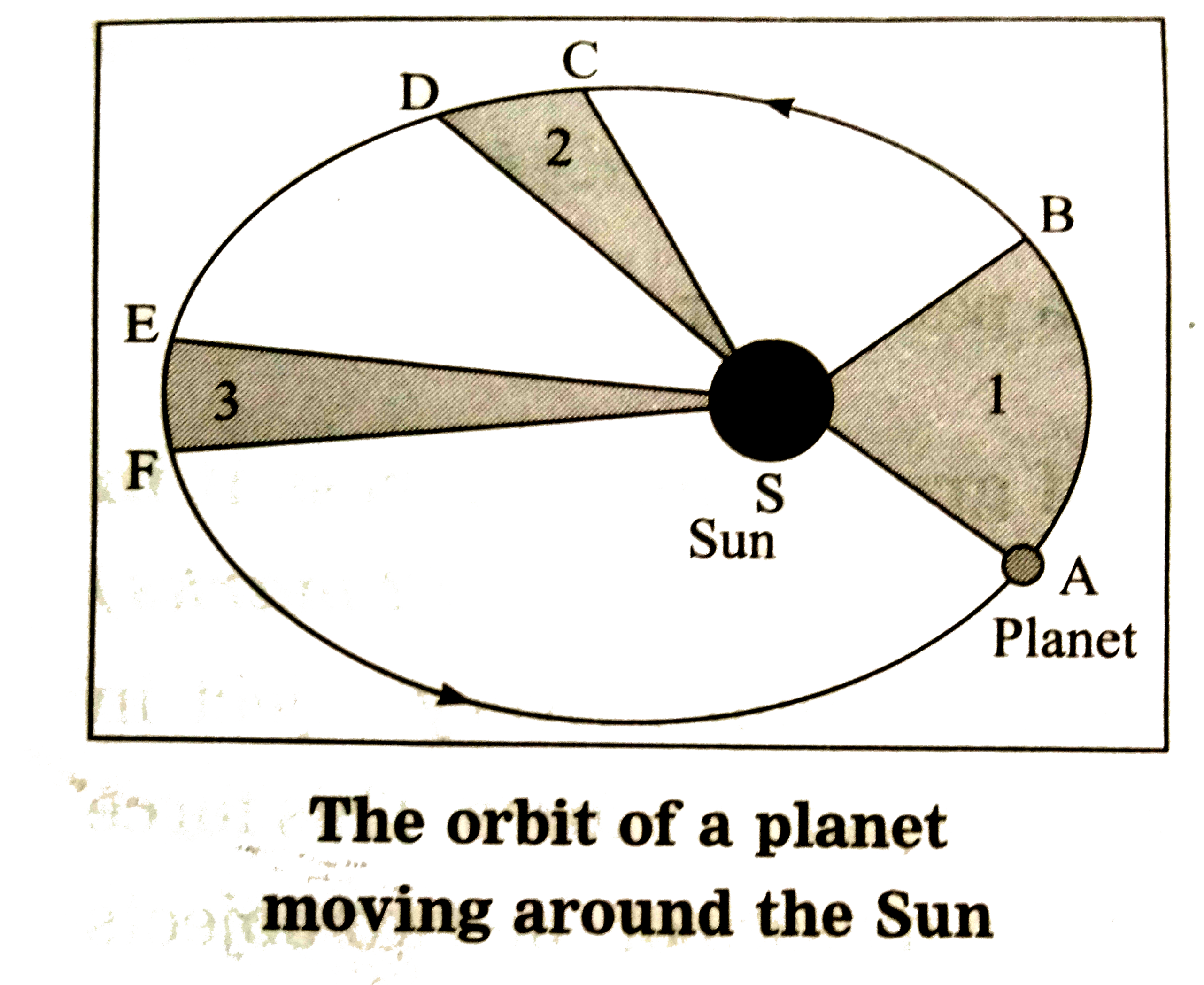
Kepler's first law: The orbit of a planet is an ellipse with the Sun at one of the foci.
The adjoining figure shows the elliptical orbit of a planet revolving around the Sun. S denotes the position of the Sun.
Kepler's second law : The line joining the planet and the Sun Sweeps equal areas in equal intervals of time.
Area ASB=area CSD=area ESF. Kepler's third law :
The square of the period of revolution of a plant around the sun is directly proportional to the cube of the mean distance of the planets from the Sun.
Thus , if r is the average distance of the planet from the Sun and T is its period of revolution , then,
T2∝r3, i.e. T2r3 =constant =K
For simplicity we shall assume the orbit to be a circle. In the adjoining figure, S denotes the poistion of the Sun, P denotes the position of a planet at a given instant and r denotes the radius of the orbit (≡ the distance of the planet from the Sun ). Here, the speed of the planet is uniform. It is
v=circumference of the circleperiod of revolution of the planet=2πrT
If m is the mass of the planet , the centripetal force exerted on the planet by the Sun (≡ gravitational force), F=mv2r
∴F=m(2πr/T)2r=4π2mr2T2r=4π2mrT2
Accordign to Kepler's third law,
T2=Kr3
∴F=42mrKr3=4π2mK(1r2)
Thus, F∝1r2 as 4π2mK is constant in a particular case.

|
Topper's Solved these Questions
- LAWS, RULES, UNITS AND DEFINITIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LAWS, RULES, UNITS AND DEFINITIONS EXERCISE - Periodic Classification of Elements
6 Videos
- LAWS, RULES, UNITS AND DEFINITIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LAWS, RULES, UNITS AND DEFINITIONS EXERCISE - Chemical Reactions and Equations
20 Videos
- HEATBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - HEATEXERCISE - NUMERICAL PROBLEMS FOR PRACTICE
12 Videos
- LENSESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - LENSESEXERCISE - Numerical Problems For Practice
20 Videos
Similar Questions
Knowledge Check
Forces which obey inverse square law are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDBoth (1) & (2)Which of the following is not the inverse square law force?
AElectric forceBGravitational forceCNuclear forceDMagnetic force between two poles
Do electromagnetic forces obey inverse square law?
View SolutionName the forces which obey inverse square law.
View SolutionWhich of the kepler's laws of planetary motion led Newton to establish the inverse-sguare rule for gravitational force between two bodies
View SolutionDo cohesive and adhesive forces obey inverse square law?
View SolutionNewtons law of gravity and force
View SolutionWhich of kepler's laws led N ewt on to inverse square rule for gravitational force ?
View Solution
