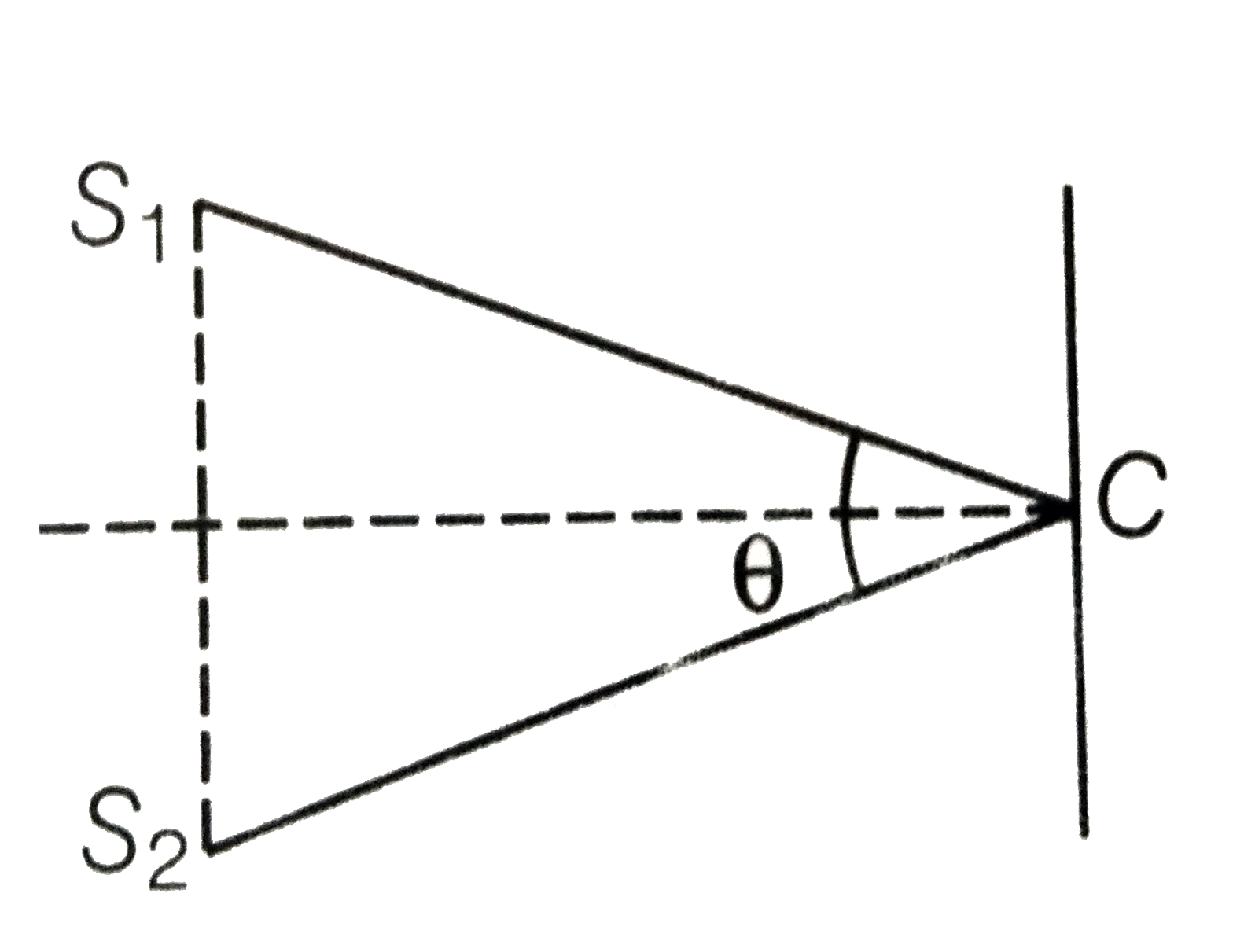
Young's double slit experimental arrangement is shown in figure. If la

In a Young’s double slit experiment, the slit separation is $0.2 c m$ , the distance between the screen and slit is 1 m . Wavelength of the light used is $5000 Å$ . The distance between two consecutive dark fringes (in mm ) is
A $2 \times 10^{- 5} m$
B $2 \times 10^{- 3} m$
C $0.2 \times 10^{- 3} m$
DNone of these
In Young's double slit experiment, the distance between the two slits is $0.1 m m$ and the wavelength of light used is $4 \times 10^{- 7} m$ . If the width of the fringe on the screen is 4 mm , the distance between screen and slit is
A $0.1 m m$
B1 cm
C $0.1 c m$
D1 m
Let $S_{1}$ and $S_{2}$ be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle $∠ S_{1} P S_{2} = θ$ , then fringe width for the light of wavelength $λ$ will be
A $λ / θ$
B $λ θ$
C $2 λ / θ$
D $λ / 2 θ$

Young's double slit experimental arrangement is shown in figure. If $λ$ is the wavelength of light used and $∠ S_{1} C S_{2} = θ$ , then the fringe width will be