Young's modulus of a rod is AgL22l for which elongation is λ due to its own weight when suspended from the ceiling. L is the length of the rod and A is constant, which is:
area
mass per unit length
mass per unit length per unit area
area per unit mass
The correct Answer is:C
Elongation in (dx) at distance x from lower end
=(WAY)dx=(mgxL)(dxAY)
Increase in length due to own weight
I=∫L0mgxdxLAY=mgL2A1Y
=(λA1)gL22l=AgL22l
Where A=λA1=mass per unit length per unit area.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Bulk Modulus And Shear Modulus29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Elasticity And Work Done In Stretching A Wire25videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
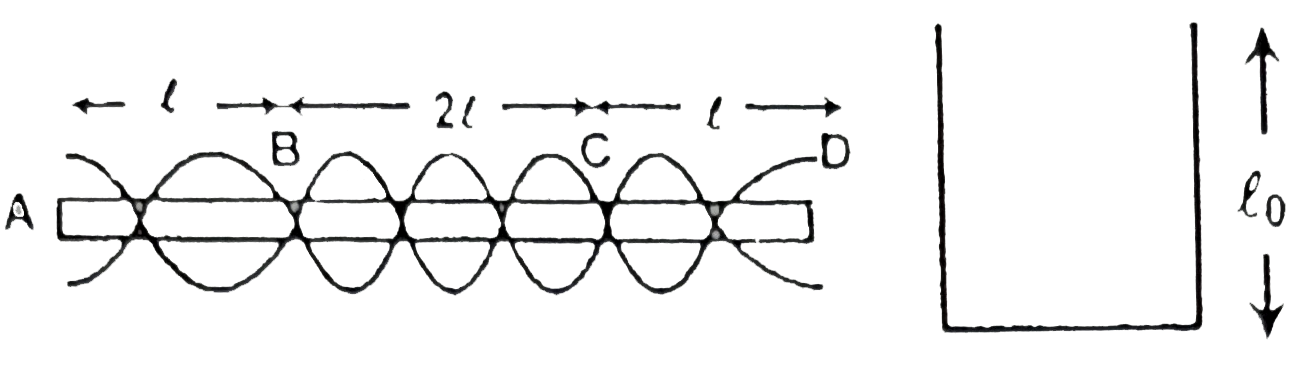
A closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]
 View Solution
View SolutionYoung's Modulus||Modulus OF Rigidity||Bulk Modulus||Energy Density||Elongation OF Rod Due to Own Weight
View Solution
Knowledge Check
- Question 1 - Select One
A string of length L and radius r elongated by x due to its own weight, when suspended from the ceiling from its one end. If another string of same material, same length and radius double the initial is suspended from its one end then elongation due to its own weight will be
A4xBx2C2xDx - Question 2 - Select One
A uniform rod of length L, has a mass per unit length λ and area of cross section A. The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
A3λgL2AlBλgL22AlC2λgLAlDλgL2Al - Question 3 - Select One
The Young's modulus of a rubber string 8 cm long and density 1.5kg/m3 is 5×108N/m2 is suspended on the ceiling in a room. The increase in length due to its own weight will be-
A9.6×10−5mB9.6×10−11mC9.6×10−3mD9.6m
A bar of mass m and length l is hanging from point A as shown in figure. Find the increase in its length due to its own weight. The young's modulus of elasicity of the wire is Y and area of cross-section of the wire is A.
 View Solution
View SolutionA copper rod length L and radius r is suspended from the ceiling by one of its ends. What will be elongation of the rod due to its own weight when and Y are the density and Young's modulus of the copper respectively?
View SolutionA heavy rope is suspended from the ceiling of a room. If ϕ is the density of the rope, L be its original length and Y be its. Young's modulus, then increase ΔL in the length of the rope due to its own weight is
View SolutionIf Young's modulus of the material of a rod is Y and density is ρ then time taken by sound wave to travel l length from bottom is
View SolutionA spring is made of material of Young's modulus 1011N/m2. When a weight of 10 kg is suspended vertically the elongation produced in the spring is 4 mm. If the load is reduced to half the elongation in the spring will be
View Solution

