The correct Answer is:A, B, C
(A )∵A=⎡⎢⎣12a014001⎤⎥⎦
∴A2=⎡⎢⎣12a014001⎤⎥⎦⎡⎢⎣12a014001⎤⎥⎦=⎡⎢⎣142a+8018001⎤⎥⎦
∴A3=⎡⎢⎣142a+8018001⎤⎥⎦⎡⎢⎣12a014001⎤⎥⎦=⎡⎢⎣163a+240112001⎤⎥⎦
Similarly , we get
An=⎡⎢
⎢⎣12nna+8∑n−1r=0r014n001⎤⎥
⎥⎦=⎡⎢⎣11820070136001⎤⎥⎦[given]
⇒2n=18⇒n=9
∴na+8n−1∑r=0r=2007⇒9a+88∑r=0r=2007
⇒9a+8⋅(8×92)=2007⇒9a=2007−288=1719
∴a=191
Hence, n+a=9+191=200
(B) n=adjA
⇒b=|B|=|adjA|=|A|2=A2=9⇒a=3,b=9
and 12λ=39+3293+3395+...+∞
=13+181+127×81+...+∞=131−127=926
⇒λ=913
Now, (ab2+a2b+1)λ=(3×81+9×9+1)×913=225
(C) det(A)=∣∣
∣
∣∣abcpqr111∣∣
∣
∣∣=∣∣
∣
∣∣ap1bq1cr1∣∣
∣
∣∣=2×12∣∣
∣
∣∣ap1bq1cr1∣∣
∣
∣∣
=2× Area of the triangle with vertices
(a, p), (a, q) and (c, r) with sides 5, 6, 7
=2×√s(s−a)(s−b)(s−c)=2×6√6=12√6
Hence, det(B2)=(12)3det(b)=18det(A2)
=18(detA)2=18(12√6)2=108
Similar Questions
The area of the shaded part in the figure given below is ______.
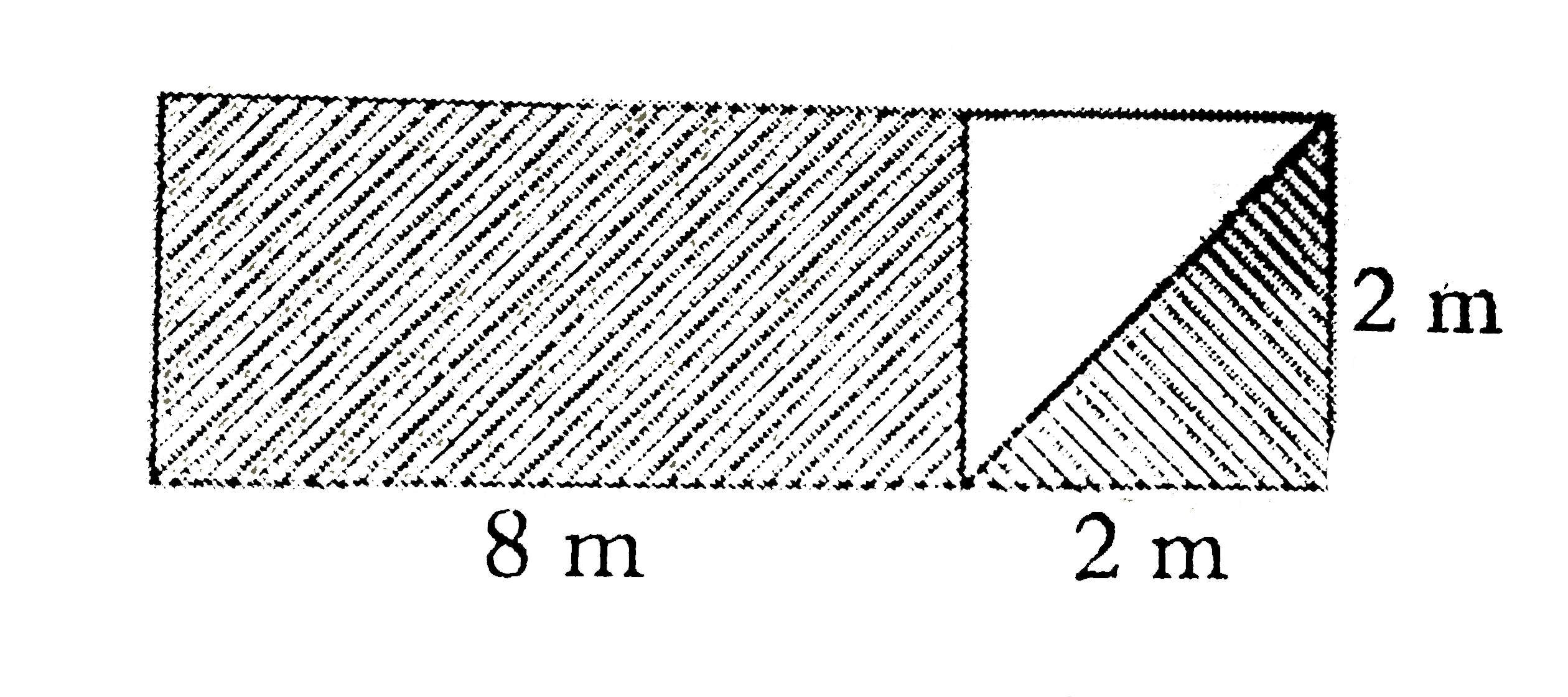
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View SolutionMatch column I with column II:
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C18_E01_003_Q01.png" width="80%"gt
View Solution

