The correct Answer is:C
a.
Thus, triangle is right angled.
b.
.
c.
or
or
( which is not possible as )
Thus, triangle is equilateral.
d.
Topper's Solved these Questions
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Numerical Value Type )
38 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Single correct Answer Type (Archives) JEE Main
5 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Exercise (Linked Comprehension Type)
20 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type
6 Videos
Similar Questions
If f(θ)=1−sin2θ+cos2θ2sin2θ then value off(11o).f(34o) is
View SolutionLet AandB denote the statements
A:cosα+cosβ+cosγ=0
B:sinα+si∈β+sinγ=0
If cos(β−γ)+cos(γ−α)+cos(α−β)=−32,
then
View SolutionIf sinα=Asin(α+β),A≠0, then
The value of tanα is
View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
View SolutionIf sec x + tan x =22/7 , find the value of tanx/2
View SolutionIdentify the cell organelle 'A' :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_BIO_C10_E08_018_Q01.png" width="80%"gt
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
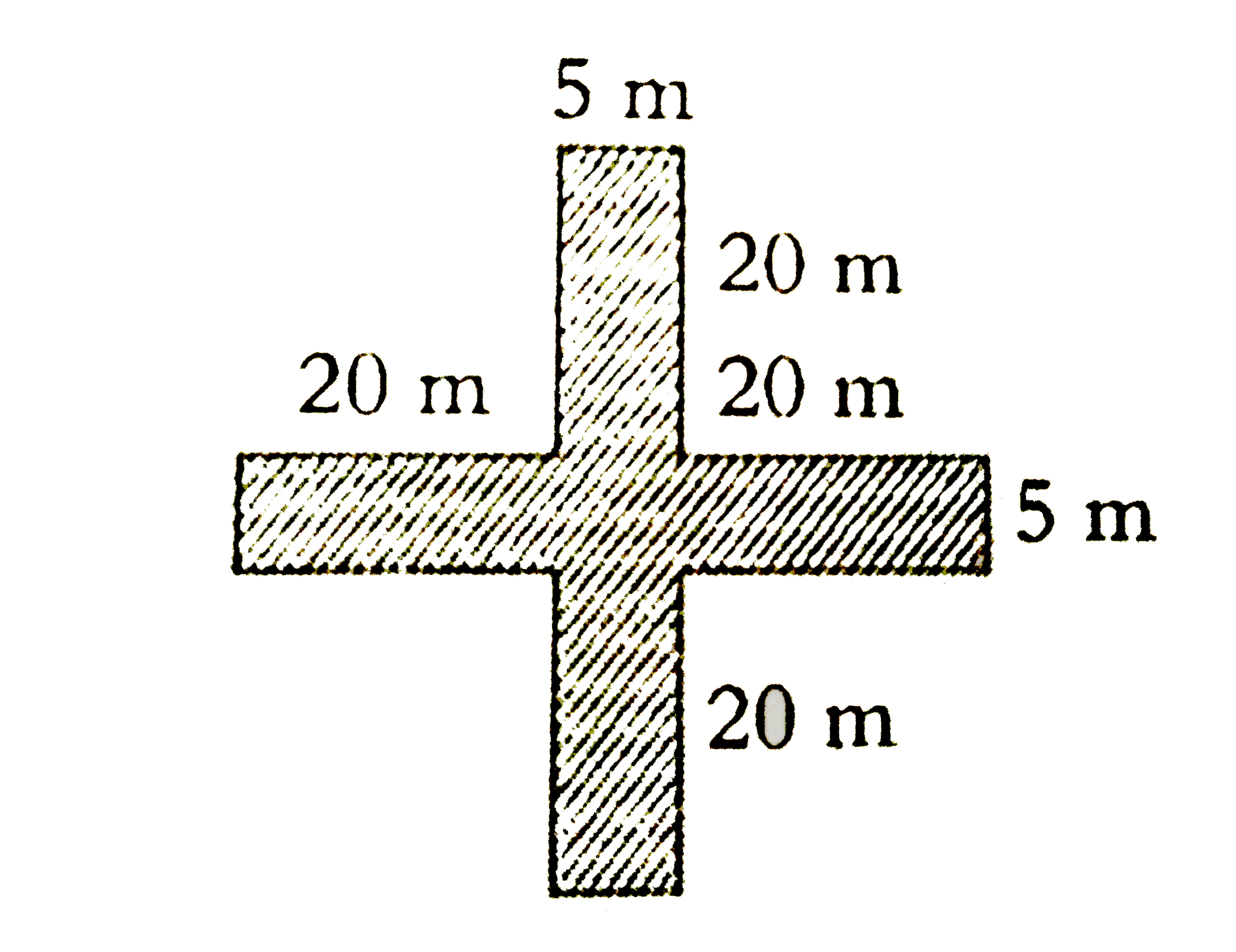
View SolutionThe area of the shaded part in the figure given below is ______.
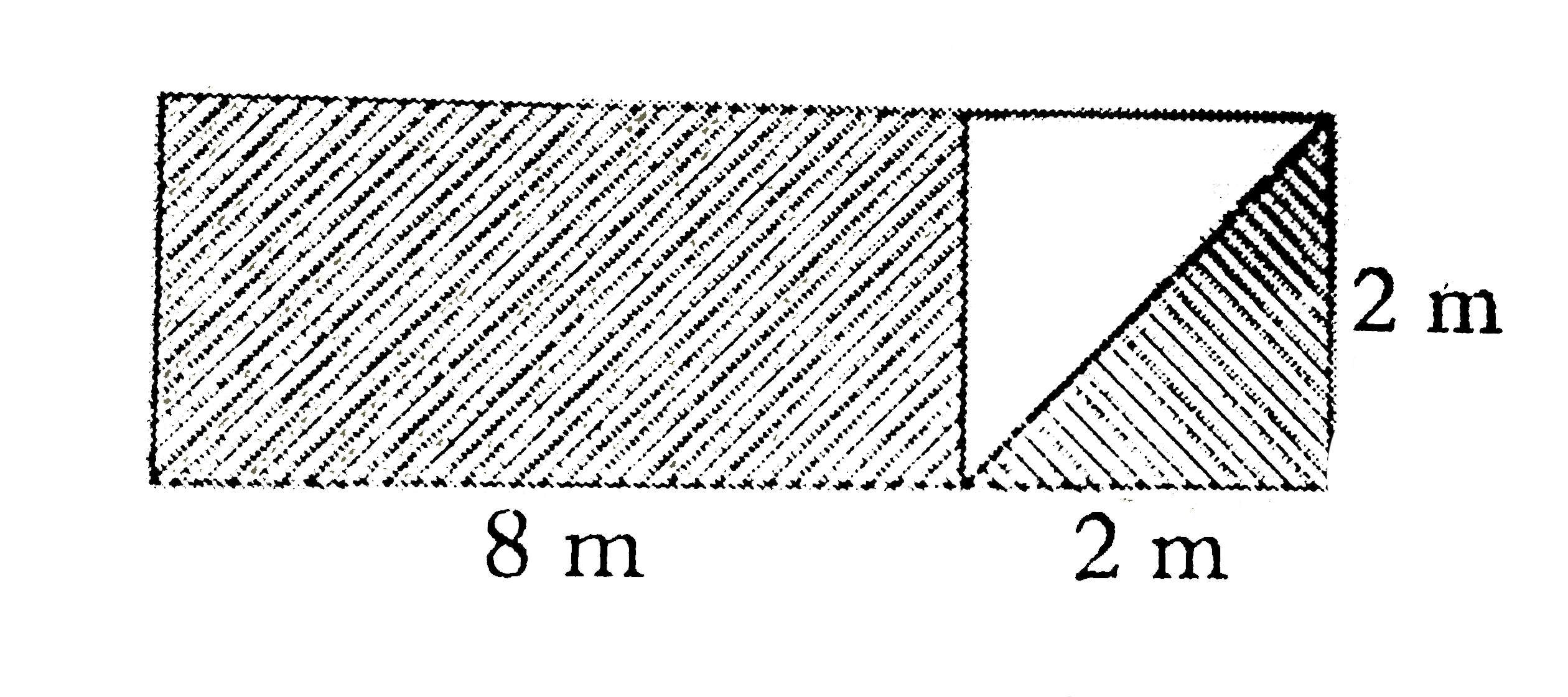
View SolutionThe inequation represented by the graph given below is :
View Solution

