The correct Answer is:.
a.
Therefore, the given equation is
or
b.
But this does not satisfy the equation because is absurd.
c. ...(i)
and so ,
Also lies in the second quadrant
Equation (i) can be rewritten as
On squaring, we get
or
or
, therefore ...(ii)
and so the general value of x is given by
d.
...(i)
Since is real when , we have
Therefore, x lies in the first quadrant. Now Eq. (i) gives
Topper's Solved these Questions
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercises (Numerical value type)
21 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives ((JEE MAIN) Single correct Answer type)
2 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercises (Linked comprehension type)
14 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - ARCHIVES INTEGER TYPE
1 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE
38 Videos
Similar Questions
Number of values of p for which equation sin^3x+1+p^3-3psinx=0(p >0) has a root is ________
View SolutionIf 0≤x≤2π, then the number of real values of x, which satisfy the equation cosx+cos2x+cos3x+cos4x=0, is
View SolutionFind the value of :- tan780∘
View SolutionIf the distance between the plane ax 2y + z = d and the plane containing the lines x−12=y−23=z−34 and x−23=y−34=z−45 is √6 , then value of |d| is
View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
View SolutionIdentify the cell organelle 'A' :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_BIO_C10_E08_018_Q01.png" width="80%"gt
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
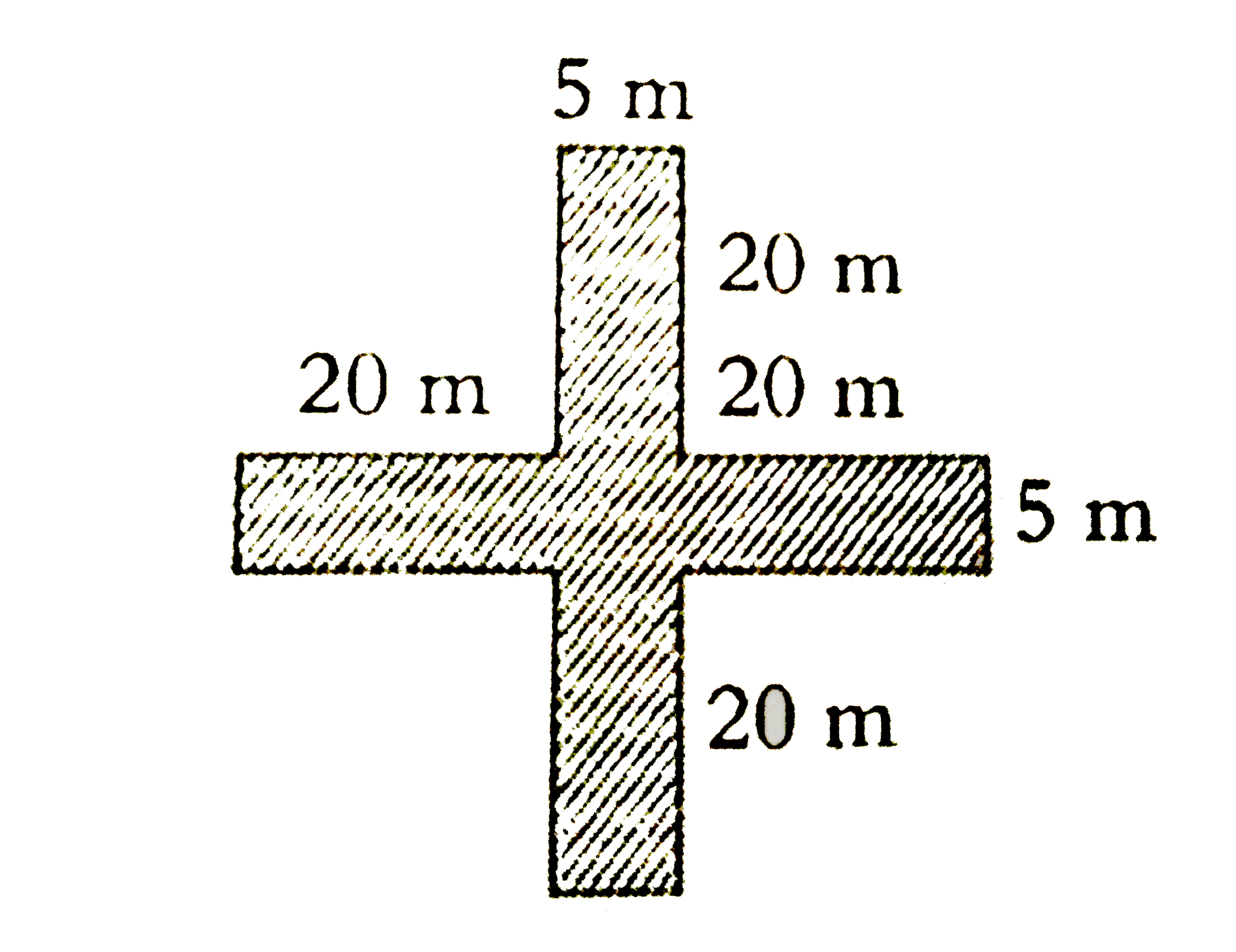
View SolutionThe area of the shaded part in the figure given below is ______.
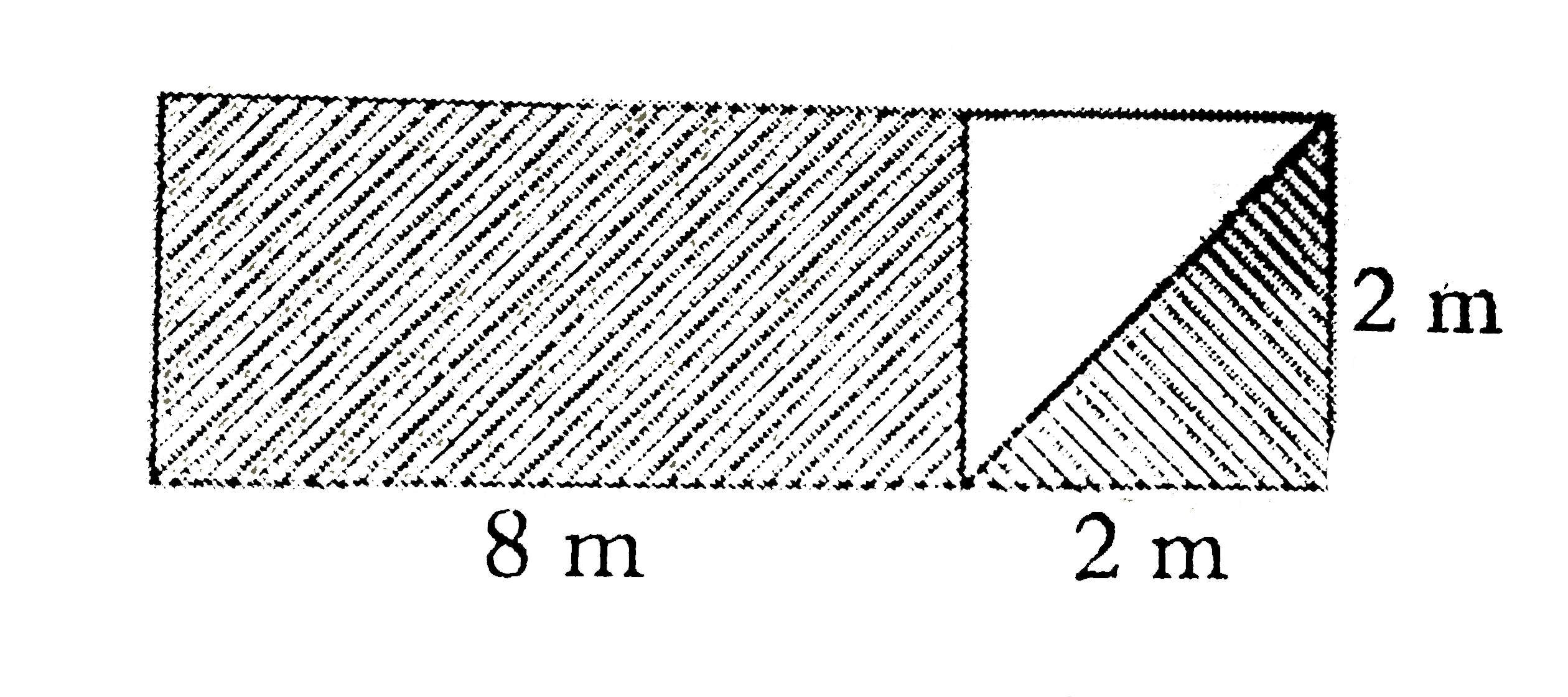
View SolutionThe inequation represented by the graph given below is :
View Solution

