The correct Answer is:(A)→(q,r,s),(B)→(p),(C)→(q)
A→(q,r,s),B→(p),C→(q)
(A)∵(d+a−b)2+(d+b−c)2=0
which is possible only when
d+a−b=0,d+b−c=0
⇒b−a=c−b
⇒2b=a+c
∴a,b and c are in AP ……….i
∵a(b−c)+b(c−a)+c(a−b)=0
∴x=1 is a root of
a(b−c)x2+b(c−a)x+c(a−b)=0........ii
Given roots[Eq (ii) ] are equal.
∴1×1=c(a−b)a(b−c)
⇒a(b−c)=c(a−b)
or b=2qca+c
∴a,b and c are in HP ............iii
From Eq. i and ii we get
a=b=c
∴a,b and c are in AP, GP and HP
(B)∵x3−3x2+3x−1=0
⇒(x−1)3=0
∴x=1,1,1
⇒ Common root x=1
∴a(1)2+b(1)+c=0
⇒a+b+c=0
(C)Given bx2+(√(a+c)2+4b2)x+(a+c)≥0
=∴D≤0
⇒(a+c)2+4b2−4b(a+c)≤0
⇒(a+c−2b)2≤0
or (a+c−2b)2=0
∴a+c=2b
Hence a, b and c are in AP.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Subjective Type Questions)
24 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matching Type Questions)
2 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
1 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
Statement -1 If the equation (4p−3)x2+(4q−3)x+r=0 is satisfied by x=a,x=b nad x=c (where a,b,c are distinct) then p=q=34 and r=0
Statement -2 If the quadratic equation ax2+bx+c=0 has three distinct roots, then a, b and c are must be zero.
View SolutionFor what values of m the equation (1+m)x2−2(1+3m)x+(1+8m)=0 has (m∈R)
(i) both roots are equal
View SolutionColumn I contain rational algebraic expressions and ColumnII contains possible integers which lie in their range. Match the entries of Column I with one or more entries of the elements of Column II.

View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionIdentify the cell organelle 'A' :-
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_BIO_C10_E08_018_Q01.png" width="80%"gt
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
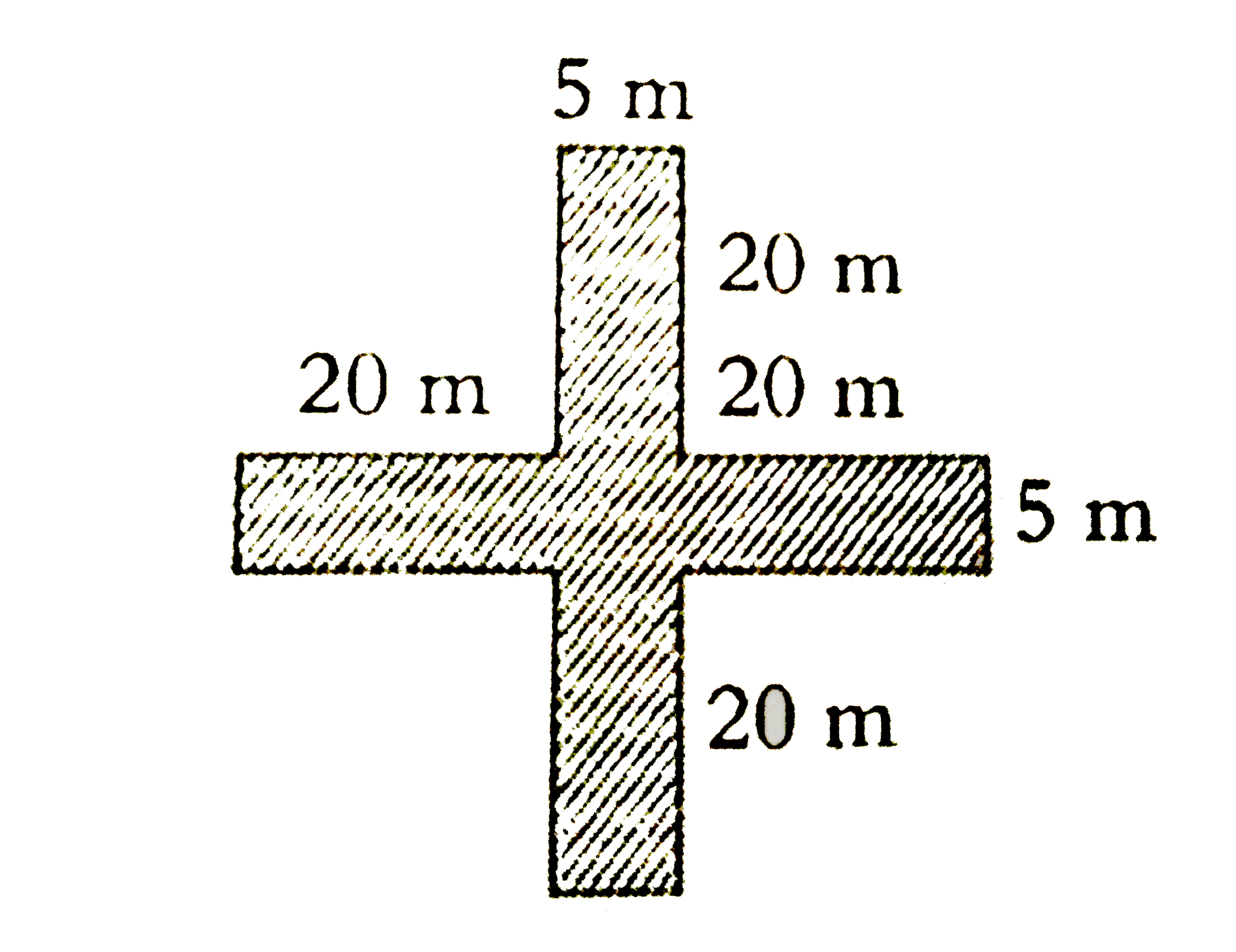
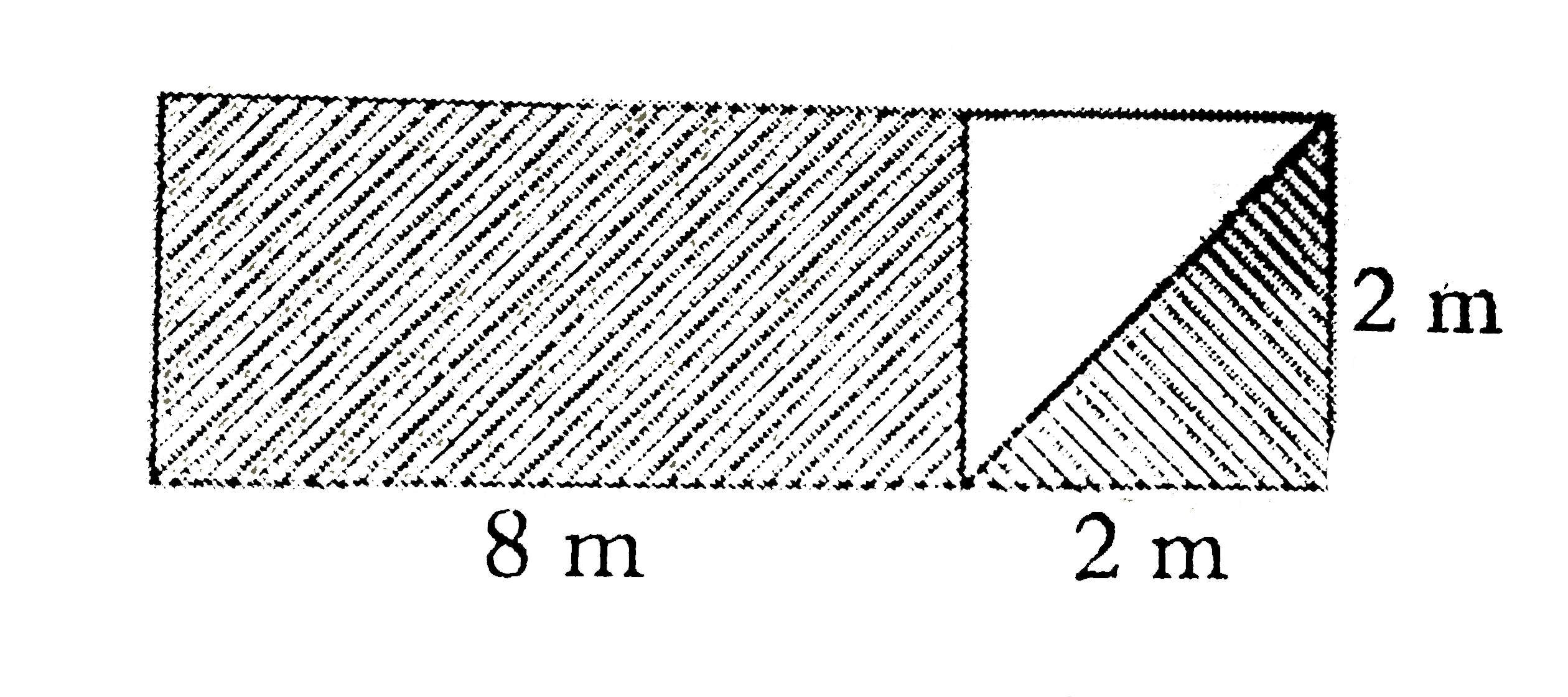
View SolutionThe area of the shaded part in the figure given below is ______.
View SolutionThe inequation represented by the graph given below is :
View Solution

