. In the following figure, PQRS is square lawn with side PQ = 42 metres. Two circular
flower beds are there on the sides PS and QR with centre at O, the intersections of its
diagonals. Find the total area of the two flower beds (shaded parts).
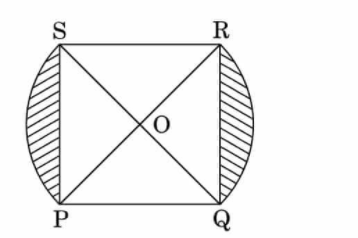
The correct Answer is:504 m2
Step by step video & image solution for . In the following figure, PQRS is square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersections of its diagonals. Find the total area of the two flower beds (shaded parts). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS RELATED TO CIRCLES BOOK - EDUCART PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLES EXERCISE - OBJECTIVE TYPE QUESTION (LONG ANSWER TYPE QUESTIONS)
19 Videos
- AREAS RELATED TO CIRCLES BOOK - EDUCART PUBLICATIONCHAPTER - AREAS RELATED TO CIRCLES EXERCISE - OBJECTIVE TYPE QUESTION (SHORT ANSWER (SA-I) TYPE QUESTIONS)
15 Videos
- ARITHMETIC PROGRESSIONSBOOK - EDUCART PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - LONG ANSWER TYPE QUESTIONS
44 Videos
Similar Questions
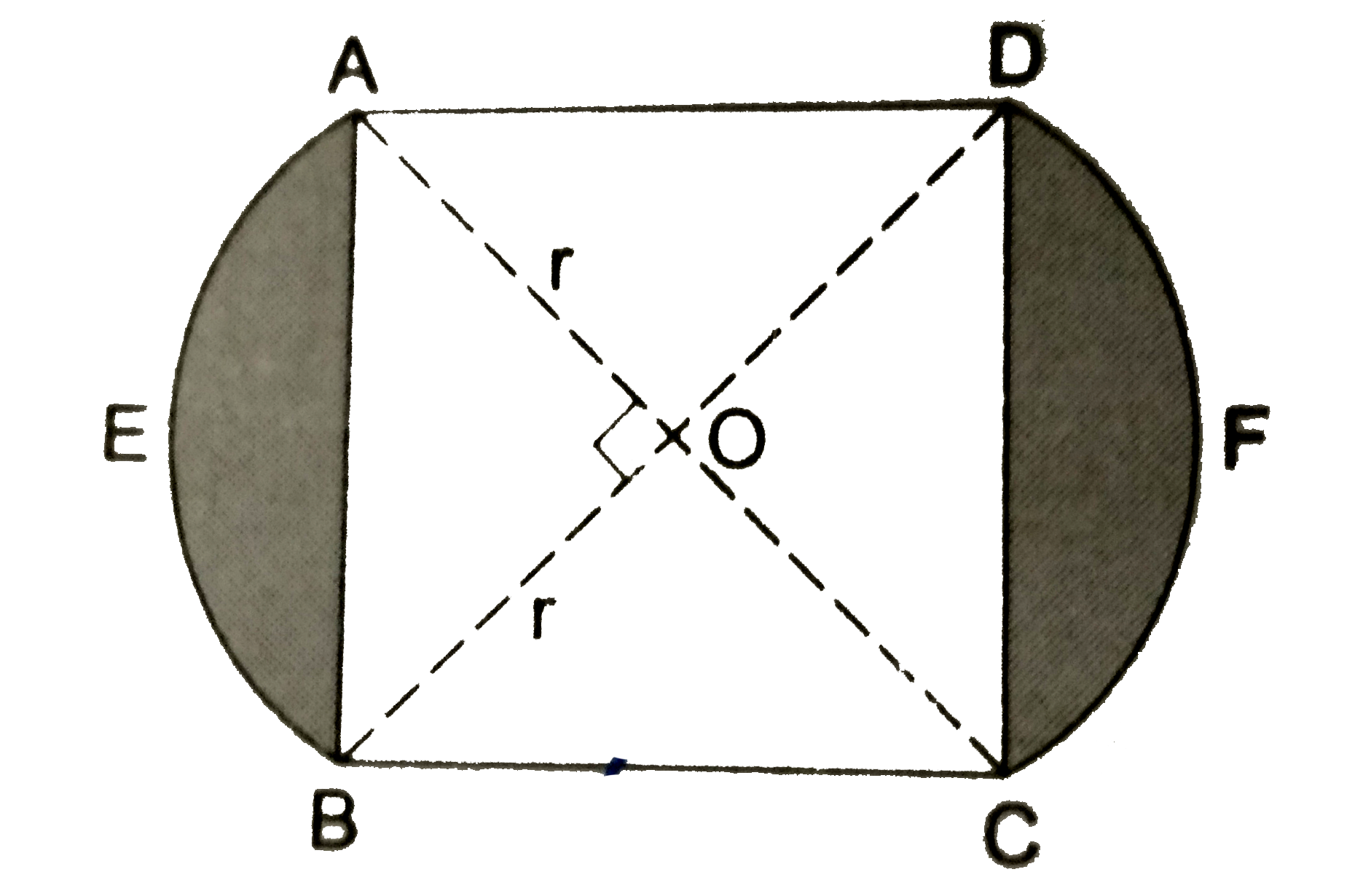
In the given figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side AB=42m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find
(i) the sum of the areas of the lawn and flower beds,
(ii) the sum of the areas of two flower beds.
View SolutionIn the given figure, PQRS is a square of side 4 cm. PSR and QSR are two quadrants of circles. Find the area of the circle touching a side and both the quadrants.
View SolutionThere are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
View SolutionIt is proposed to add to a square lawn measuring 58cm on a side, two circalar ends. The centre of each circle is the point of intersection of the diagonals of the square. Find the area of the whole lawn.
View SolutionIn Figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawns and the flower beds.
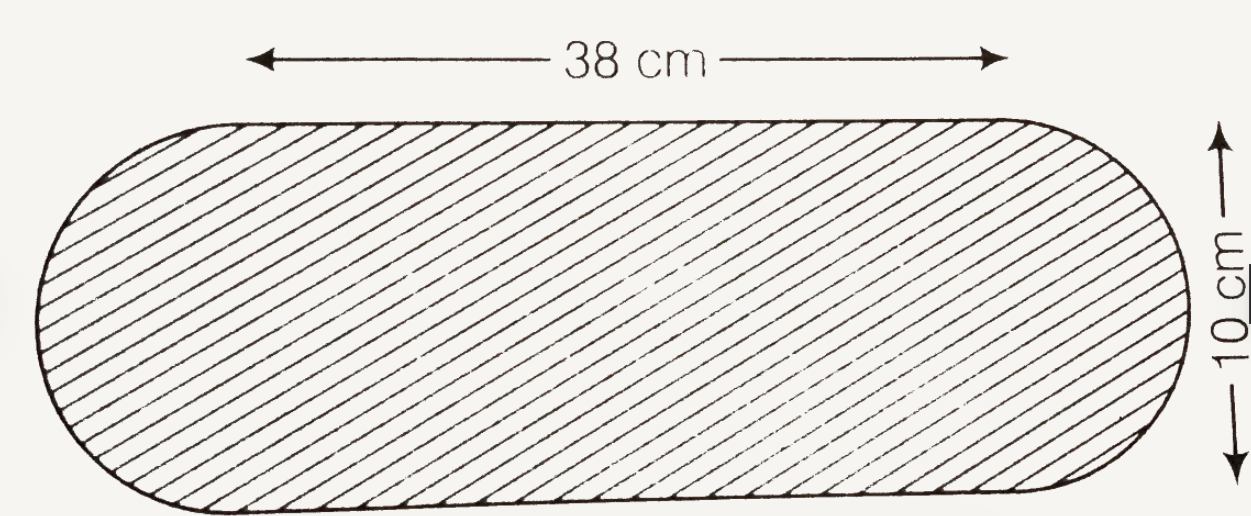
View SolutionFind the area of the flower bed (with semi-circular ends) shown in figure

View SolutionFind the area of the flower bed (with semi-circular ends) shown in figure.
View SolutionIn the adjoining figure, ABCD is a square of side 10 cm and two semicircles with side of the square as diameter. A quarter circle is also seen in figure with side of square as radius. Find the area of the square region excluding the shaded part (deepak). (Take π=3.14)

View SolutionIn the given figure, PQRS is a square whose side is 8 cm. PQS and QPR are two quadrants. A circle is placed touching both the Quadrants and the square as shown in the figure. What is the area (in cm2) of the circle?
View SolutionA square lawn with side 100 m long has a circular flower bed in the centre. If the area of the lawn, excluding the flower bed, is 8614 m2, the radius of the circular flower bed is (a) 21 m (b) 31 m (c) 41 m (d) None of these
View Solution
