यदि x−12≥2, तब x∈
A
(1, 2)
B
(0, 1)
C
[5,∞)
D
(1,∞)
Video Solution
Text Solution
The correct Answer is:C
We have,
x−1x≥2⇒x−12−2≥0⇒−1−xx≥0⇒x+1x−0≤0 …(i)
On equating x +1 and x-0 to zero, we obtain x = -1 and x = 0 as critical points. These points when plotted on number line divide it into three regions. Marking alternatively positive and negative from the right most region, we obtain the signs of x+1x for different values of x as shown in the following figure.
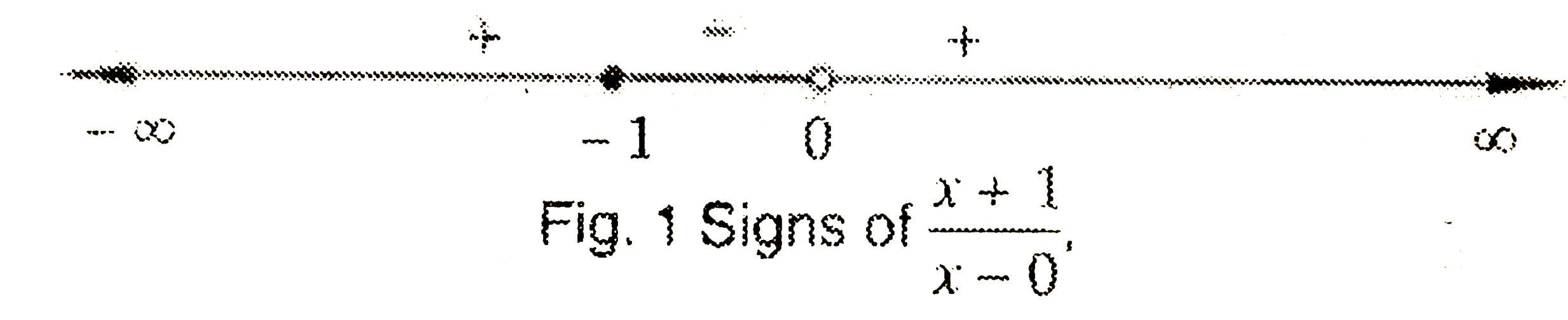 Since the expression in (i) is non-positive. So, the solution set of inequation (i) is [-1, 0].
Since the expression in (i) is non-positive. So, the solution set of inequation (i) is [-1, 0].
|
Topper's Solved these Questions
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Section I - Solved Mcqs
20 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- ALGEBRA OF VECTORSBOOK - OBJECTIVE RD SHARMACHAPTER - ALGEBRA OF VECTORSEXERCISE - Chapter Test
30 Videos
- APPLICATION OF DERIVATIVESBOOK - OBJECTIVE RD SHARMACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Illustration
6 Videos
Similar Questions
Knowledge Check
यदि (x−1)3(x+1)<0 तब x∈
A(−1,1)B(−∞,−1)C[−1,1]D(−1,∞)For L.P.P. maximize z=4x1+2X2 subject to 3x1+2x2≥9,x1−x2≤3,x1≥0,x2≥0 has ……
Ainfinite number of optimal solutionsBunbounded solutionCno solutionDone optimal solutionf(x)={tan−1x,|x|<π2π2−|x|,|x|≥π2 then
Af(x) has no point of local maximaBf(x) has only one point of local maximaCf(x) has exactly two points of local maximaDf(x) has exactly two points of local minima
If tan2x−3sec2x+3=0, then the value of x (0≤x≤90∘) is :
यदि tan2x−3sec2x+3=0, तब x का मान क्या है (0≤x≤90∘)
View SolutionLet f(x) be differentiable ∀x. If f(1)=-2 and f'(x)≥2∀x∈x[1,6], then:
View SolutionThe area (in sq units) of the region described by {(x,y):y2≤2xandy≥4x−1} is
View Solutionsolve : 3x−42+1≥x+14
View SolutionThe minimum value of Z=2x1+3x2, subject to the constraints 2x1+7x2≥22,x1+x2≥6,5x1+x2≥10 and x1,x2≥0, is
View Solution
