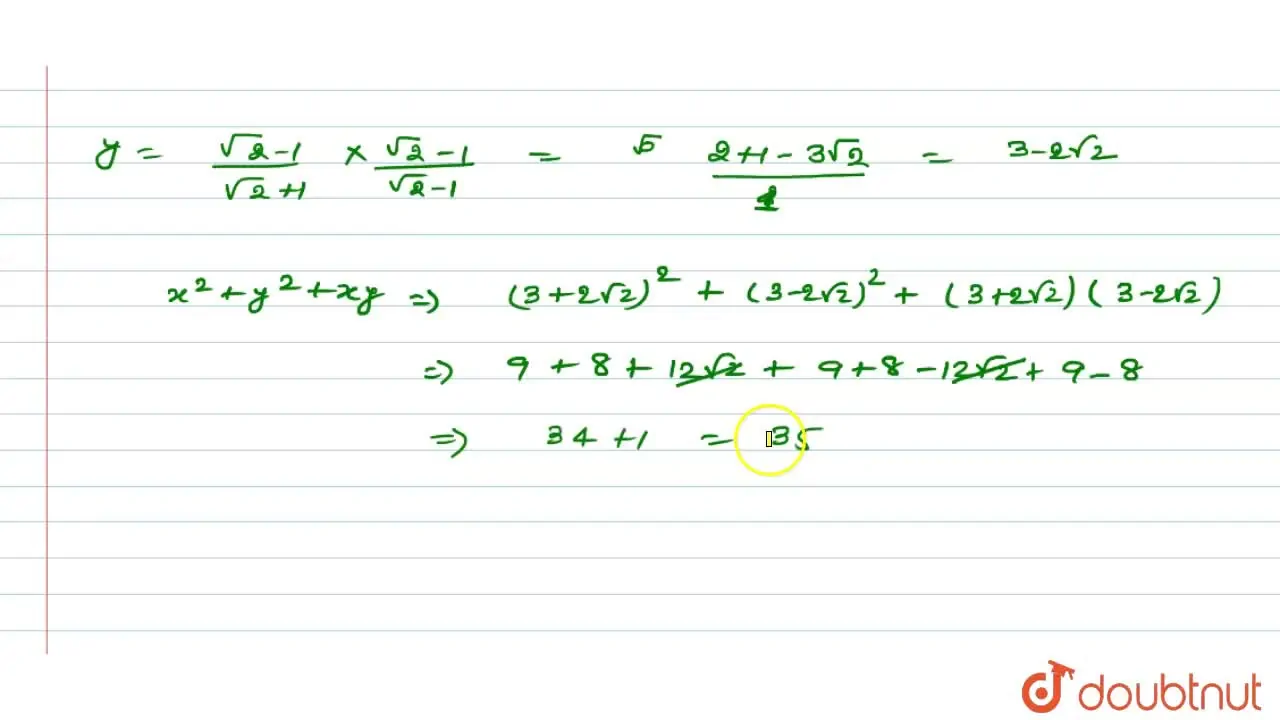यदि x=√2+1√2−1,y=√2−1√2+1 तो दिखाइए कि
x2+xy+y2=35
यहां x=√2+1√2−1=√2+1√2−1×√2+1√2+1=(√2+1)2(√2)2−12
=2+1+2√22−1=3+2√21=3=2√2
इसी प्रकार
y=√2−1√2+1=√2−1√2+1×√2−1√2−1=(√2−1)2(√2)2−12
=2+1−2√22−1=3−2√2
∴x2+xy+y2=(3+2√2)2+(3+2√2)(3−2√2)+(3−2√2)2 ltbgt =9+8+12√2+9−8+9+8−12√12=35
Related Playlists
- BOOK - MANOHAR RAYCHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1(A)15videos
संख्या पद्धति
- BOOK - MANOHAR RAYCHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1(B)5videos
संख्या पद्धति
- BOOK - MANOHAR RAYCHAPTER - वृत्त EXERCISE - प्रश्नावली 10(D)15videos
वृत्त
- BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9(D)10videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
Similar Questions
20 और 40 के बीच समस्त सम धन पूर्णांक लिखिए।
05:07View Solutionनिम्नलिखित पूर्णांकों के योगात्मक प्रतिलोम लिखिए।
−7,0,1−(a+b)04:28View Solutionमान लीजिए की कोण ABC का शीर्ष वृत्त के बहार स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएं AD और CE कटती है। सिध्द कीजिए की ∠ABC जीवाओं AC और DE द्वारा केंद्र पर अंतरित कोनो के अंतर का आधा है।
01:48View Solutionएक त्रिभुज का क्षेत्रफल 6√2 सेमी 2 है और आधार की लम्बाई 3 सेमी है। त्रिभुज की ऊंचाई होगी :
02:37View SolutionProve that sin ^ (- 1) x + cos ^ (- 1) y = (tan ^ (- 1) (xy + sqrt ((1-x ^ (2)) (1-y ^ (2)))) ) / (y sqrt (1-x ^ (2)) - x sqrt (1-y ^ (2)))
04:40View SolutionIf √1−x2+√1−y2=a(x−y), prove that dydx=√1−y21−x2
02:29View SolutionIf x=(sqrt(2)+1)/(sqrt(2)-1),y=(sqrt(2)-1)/(sqrt(2)+1) Find the value of x^(2)+y^(2)+xy
02:22View Solutionयदि x=√5+1√5−1 और y=√5−1√5+1 तो x2+xy+y2x2−xy+y2 का मान निकालें
02:33View Solutionयदि x=√3+√2√3−√2 व y=1x, तब सिद्ध कीजिए कि x2+y2+xy=99
01:10View Solutiony=√1+x2 and y'=xy1+x2
05:38View Solutiony=√1+x2:y'=xy1+x2
06:05View Solutiony=√1+x2:y'=xy1+x2
09:21View Solutiony=√1+x2:y'=xy1+x2
01:57View Solutionx=√3+1√3−1 এবং y=√3−1√3+1 হয়, x2−xy+y2x2+xy+y2-এর সরলতম মান নির্ণয় করো।
04:32View SolutionIf √1−x2+√1−y2=a(x−y), then prove that dydx=√1−y21−x2
04:19View Solution