1c∫bcacf(xc)dx=
1c∫baf(x)dx
∫baf(x)dx
c∫baf(x)dx
∫bc2ac2f(x)dx
The correct Answer is:B
To solve the integral
1c∫bcacf(xc)dx,
we will perform a substitution to simplify the integral.
Step 1: Substitution
Let t=xc. Then, we differentiate both sides with respect to x:
dtdx=1c⟹dx=cdt.
Step 2: Change of Limits
Now, we need to change the limits of integration. When x=ac:
t=acc=a.
When x=bc:
t=bcc=b.
Step 3: Rewrite the Integral
Substituting x and dx in the integral gives us:
∫bcacf(xc)dx=∫baf(t)⋅cdt.
Step 4: Factor Out Constants
Now, substituting this back into our original equation, we have:
1c∫bcacf(xc)dx=1c⋅∫baf(t)⋅cdt.
The c in the numerator and denominator cancels out:
=∫baf(t)dt.
Final Result
Thus, we conclude that:
1c∫bcacf(xc)dx=∫baf(t)dt.
Let t=xc. Then, we differentiate both sides with respect to x:
Now, we need to change the limits of integration. When x=ac:
Substituting x and dx in the integral gives us:
Now, substituting this back into our original equation, we have:
Thus, we conclude that:
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - ProblemSet (1) True and false1videos
DEFINITE INTEGRAL
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - ProblemSet (2) (Multiple Choice Questions)47videos
DEFINITE INTEGRAL
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)1videos
DEFINITE INTEGRAL
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - SELF ASSESSMENT TEST10videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - DETERMINANTS EXERCISE - Self Assessment Test19videos
DETERMINANTS
Similar Questions
Knowledge Check
- Question 1 - Select One
1c∫bcacf(xc)dx=
A1c∫baf(x)dxB∫baf(x)dxCc∫baf(x)dxD∫bc2ac2f(x)dx - Question 2 - Select One
1c∫bcacf(xc)dx=
A1c∫baf(x)dxB∫bc2ac2f(x)dxCc∫baf(x)dxD∫baf(x)dx - Question 3 - Select One
Assuming that f is everywhere continuous, 1c∫bcacf(xc)dx is equal to
A1cb∫af(x)dxBb∫af(x)dxCcb∫af(x)dxDcbc2∫ac2f(x)dx
STATEMENT 1: ∫π0sin100xcos99xdxis z ero . STATEMENT 2: ∫baf(x)dx=∫b+ca+cf(x−c)dx,and for odd function, ∫a−af(x)dx=0
View Solution1c∫baf(xc)dx=
View Solution∫b+ca+cf(x)dx is equal to:
View SolutionFor every function f (x) which is twice differentiable , these will be good approximation of
∫baf(x)dx=(b−a2){f(a)+f(b)}, for more acutare results for c∈(a,b),F(c)=c−a2[f(a)−f(c)]+b−c2[f(b)−f(c)]
When c=a+b2
∫baf(x)dx=b−a4{f(a)+f(b)+2f(c)}dx
Good approximation of ∫π/20sinxdx,isView SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
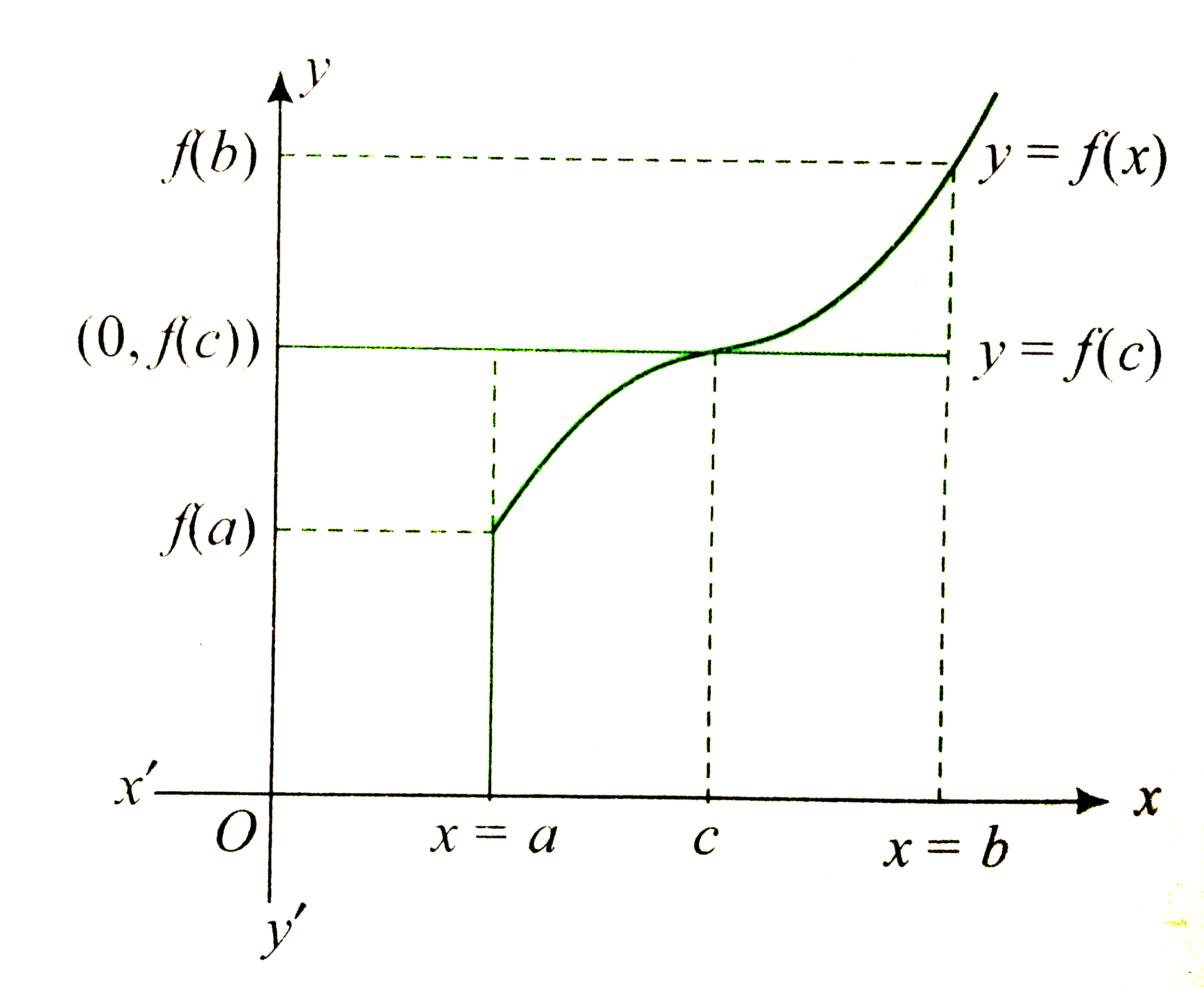
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a isView Solution
