1. Find the areas of the following figures by counting square:
To find the area of the given figure by counting squares, we will follow these steps:
1. Identify the Types of Squares:
- We categorize the squares into four types:
- Fully filled squares
- Half filled squares
- More than half filled squares
- Less than half filled squares
2. Count the Fully Filled Squares:
- Count the number of fully filled squares in the figure.
- In this case, there are 2 fully filled squares.
3. Count the Half Filled Squares:
- Count the number of half filled squares.
- Here, we find 4 half filled squares.
4. Count the More than Half Filled Squares:
- Count the number of squares that are more than half filled.
- We have 4 more than half filled squares.
5. Count the Less than Half Filled Squares:
- Count the number of squares that are less than half filled.
- There are 4 less than half filled squares.
6. Calculate the Area Contribution:
- Assign area values based on the type of square:
- Fully filled squares contribute 1 square unit each.
- Half filled squares contribute 1/2 square unit each.
- More than half filled squares contribute 1 square unit each.
- Less than half filled squares contribute 0 square units each.
7. Calculate Total Area:
- Total area = (Number of fully filled squares × Area of fully filled) +
(Number of half filled squares × Area of half filled) +
(Number of more than half filled squares × Area of more than half filled) +
(Number of less than half filled squares × Area of less than half filled)
- Plugging in the values:
- Total area = (2 × 1) + (4 × 1/2) + (4 × 1) + (4 × 0)
- Total area = 2 + 2 + 4 + 0
- Total area = 8 square units.
Final Answer:
The area of the figure is 8 square units.
---
- We categorize the squares into four types:
- Fully filled squares
- Half filled squares
- More than half filled squares
- Less than half filled squares
- Count the number of fully filled squares in the figure.
- In this case, there are 2 fully filled squares.
- Count the number of half filled squares.
- Here, we find 4 half filled squares.
- Count the number of squares that are more than half filled.
- We have 4 more than half filled squares.
- Count the number of squares that are less than half filled.
- There are 4 less than half filled squares.
- Assign area values based on the type of square:
- Fully filled squares contribute 1 square unit each.
- Half filled squares contribute 1/2 square unit each.
- More than half filled squares contribute 1 square unit each.
- Less than half filled squares contribute 0 square units each.
- Total area = (Number of fully filled squares × Area of fully filled) +
(Number of half filled squares × Area of half filled) +
(Number of more than half filled squares × Area of more than half filled) +
(Number of less than half filled squares × Area of less than half filled)
- Plugging in the values:
- Total area = (2 × 1) + (4 × 1/2) + (4 × 1) + (4 × 0)
- Total area = 2 + 2 + 4 + 0
- Total area = 8 square units.
The area of the figure is 8 square units.
Topper's Solved these Questions
Similar Questions
Find the area of the following figures

View SolutionFind the area of the following figures.
View SolutionFind the area of each of the following figures.

View SolutionFind the area of the given figure.
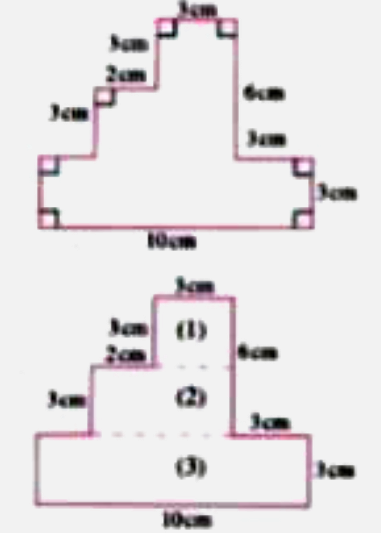
View SolutionFind the area of the given figure.
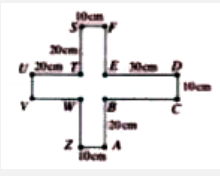
View SolutionFind the area of the following regular hexagon Figure
View SolutionFind the area of the figure given below.

View SolutionFind the area of the shaded region in figure.

View SolutionFind the area of the field shown in Figure by dividing it into a square, a rectangle and a trapezium.
View SolutionFind the area of the shaded region in Figure.
View Solution
