1∘ is approximately equal is
0.001746 radians
0.01746 radians
0.0001746 radians
0.1746 radians
To convert 1 degree into radians, we can follow these steps:
Step 1: Understand the conversion formula
The formula to convert degrees to radians is:
Radians=Degrees×π180
Step 2: Substitute the value
For the given question, we need to convert 1 degree into radians:
Radians=1×π180
Step 3: Simplify the expression
This simplifies to:
Radians=π180
Step 4: Calculate the numerical value
Using the approximate value of π≈3.14:
Radians≈3.14180≈0.01745
Step 5: Round off the answer
Rounding off to four decimal places, we get:
Radians≈0.0175
Final Answer:
Thus, 1∘ is approximately equal to 0.0175 radians.
---
The formula to convert degrees to radians is:
Radians=Degrees×π180
For the given question, we need to convert 1 degree into radians:
Radians=1×π180
This simplifies to:
Radians=π180
Using the approximate value of π≈3.14:
Radians≈3.14180≈0.01745
Rounding off to four decimal places, we get:
Radians≈0.0175
Thus, 1∘ is approximately equal to 0.0175 radians.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A typical 3-D printer creates object by laying down layers of ink one on top of another. The average thckness of layer depends on the caliber of the printer. For one particular 3-D printer, the average thickness of a layer is 102μm (micrometers). When creating a 1-inch cube, the printer takes 6 second to lay down each layer of ink. Approximately how long should it take this printer to create a 1-inch cube? (There are 1,000,000 micrometers in a meter, and 1 inch is approximately equal to 0.0254 meters.)
A12 minutesB25 minutesC40 minutesD1 hour, 6 minutes1 radian is approximately equal to
A57∘16'B47∘18'30''C53∘17'45''D43∘16'
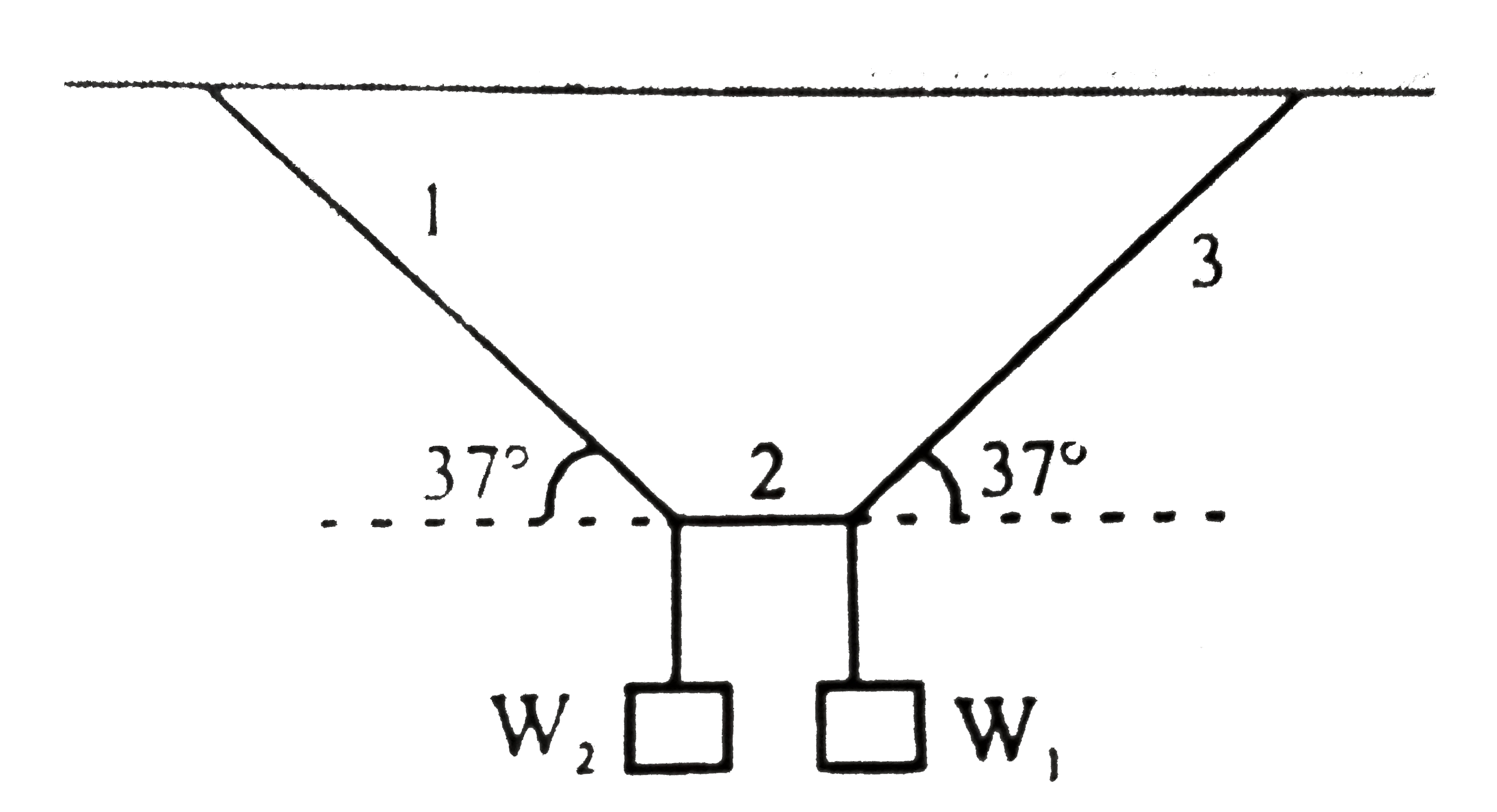
In a given figure system is in equlibrium, If W1= 300 N. Then W2 is approximately equal to
View SolutionThe percentage weight of Zn in which vitriol [ZnSO4⋅7H2O] is approximately equal to (at. Mass of Zn =65 , S= 32, O=16 and H=1)
View SolutionIf (1−3x)1/2+(1−x)5/3√4−x is approximately equal to a+bx for small values of x, then (a,b) is (a) (1,3524) (b) (1−35/24) (c) (2,3512) (d) (2,−3512)
View SolutionOne litre-atmosphere is approximately equal to
View SolutionThe cut-in voltage of a germanium diode is approximately equal to
View SolutionWhich of the following triads have approximately equal size ?
View Solution
