different books and different pens are given to boys so that each gets equal number of things. The probability that the same boy does not receive both the pens is
The correct Answer is:C
the number of ways in which any one boy gets both the pens
Required probability
Topper's Solved these Questions
- PROBABILITYBOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Multiple Correct Answer
13 Videos
- PROBABILITYBOOK - CENGAGECHAPTER - PROBABILITYEXERCISE - Comprehension
2 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - CENGAGECHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise
9 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
37 Videos
Similar Questions
Knowledge Check
10 different books and 2 different pens are given to 3 boys so that each gets equal number of things. The probability that the some boy does not receive both the pens, is
A8/11B7/11C2/3D6/11If 15 boys of different ages are distributed into 3 groups of 4,5, and 6 boys randomly then the probability that three youngest boys are in different groups is
A2491B7191C6791D209110 boys are randomly divided into two grops containing 5 boys each. The probability that the two tallest boys are in the different groups is:
A104B49C59D15
5 different Engineering, 4 different Mathematics and2 different Chemistry books are placed in a shelf at random. The probability that the books of each kind are all together is
View Solution10 boys and 2 girls are divided into 3 groups of 4 each. The probability that the girls will be in different groups is
View SolutionIn how many ways, 7 different books are given to 2 students one get 4 books and another gets 3 books?
View Solution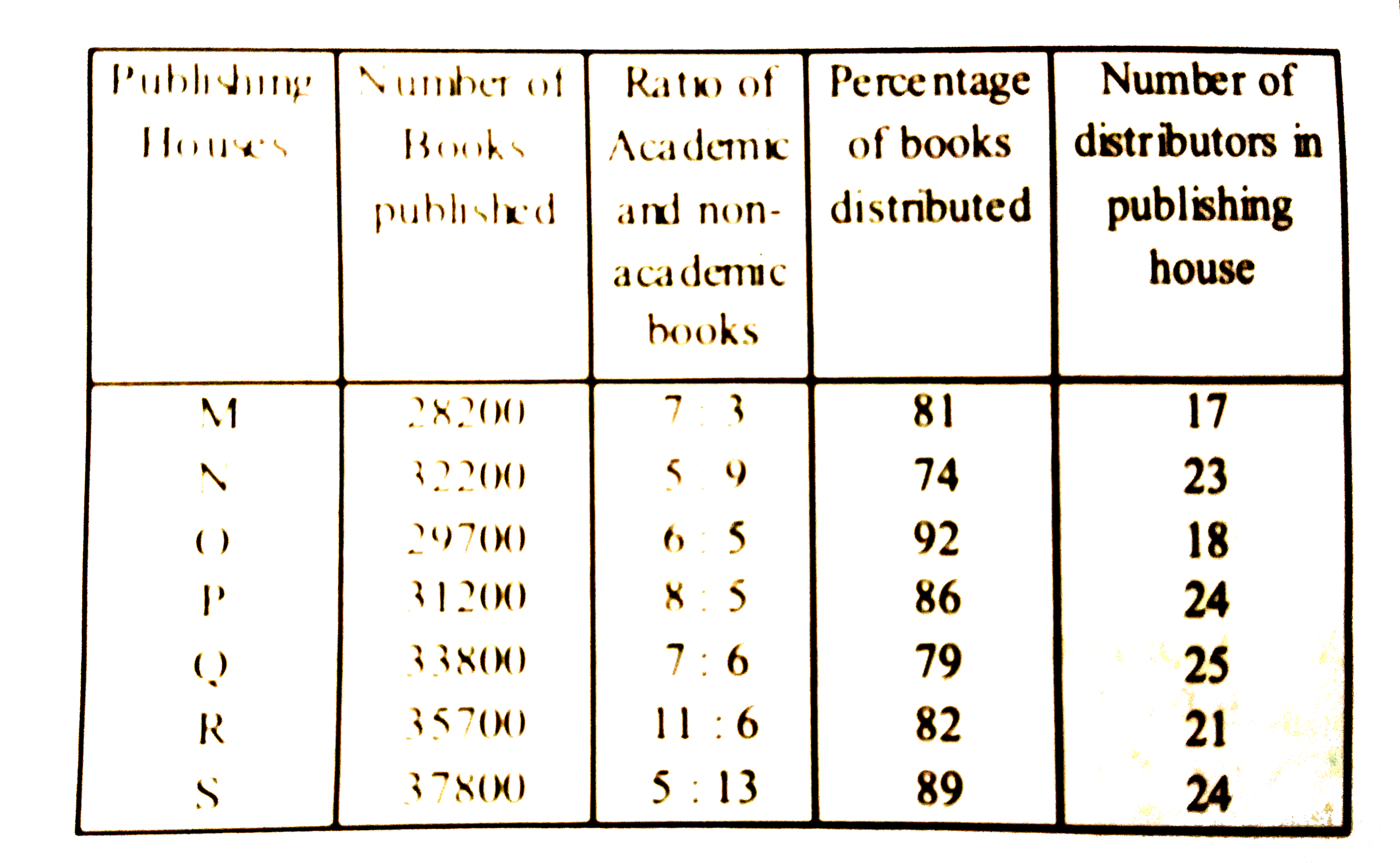
How many books were given to each distributor by publisher Q if each publisher gets equal number of books ?
View SolutionThe Number of ways in which five different books to be distributed among 3 persons so that each person gets at least one book, is equal to the number of ways in which? 5 persons are allotted 3 different residential flats so that each person is allotted at most one flat and no two persons are allotted the same flat
View Solution
