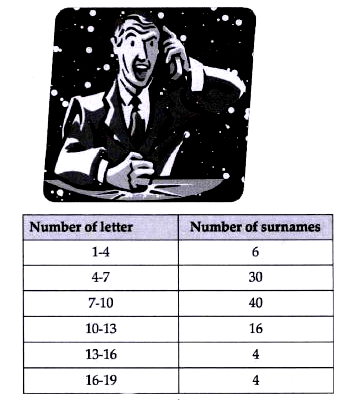
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.

1) median class = 7 - 10
Class size, h = 3
Lower limit of median class, l = 7
Frequency of median class, f = 40
Cumulative frequency of class preceding median class,cf=36
Median = l+[n2−cff]×h
= 7+[50−3640]×3
= 7+(1440)×3
= 7+2120
= 7+1.05
=8.05
2)Now, we will find the mean.
Class mark, xi= (Upper class limit + Lower class limit)/2
Taking assumed mean, a = 11.5
Σfi = 100 andΣfiui = -106
Class size, h=3
Mean, (x) = a+(ΣfiuiΣfi)×h
=11.5+(−106100)×3
=11.5−318100
=11.5−3.18
8.32
3)it can be observed that the maximum class frequency is 40, belonging to class interval 7−10.
Class size, h=3
Modal class =7−10
Lower limit of modal class, l=7
Frequency of modal class, f1=40
Frequency of class preceding modal class, f0=30
Frequency of class succeeding the modal class, f2=16
Mode =l+[f1−f02f1−f0−f2]×h
=7+[40−302×40−30−16]×3
=7+(1034)×3
=7+1517
=7+0.88
=7.88
=8.05
Similar Questions
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
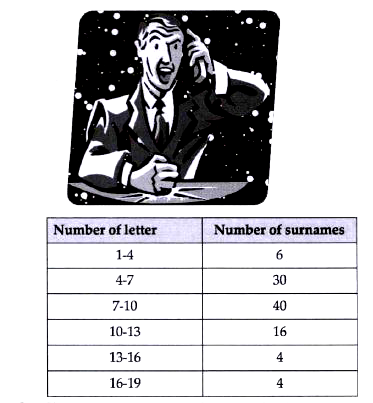
What is the upper limit of modal class?View Solution100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
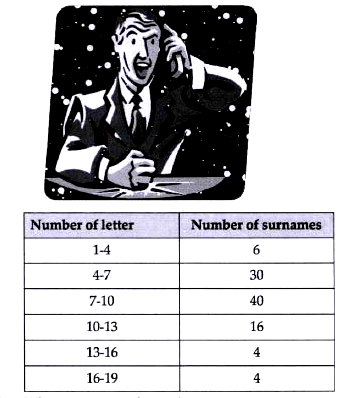
What is the upper limit of median class?View Solution100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Sum of lower limit of median and modal class is:View Solution101 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

Write the class interval in which the maximum number of surnames lie.View Solution100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:
(i) Draw a histogram
(ii) write the class interval in which maximum number of surnames lie .
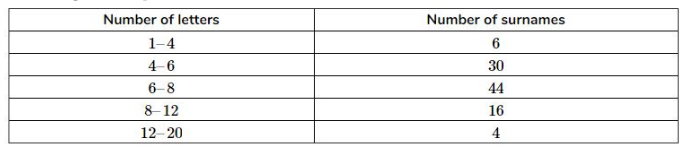 View Solution
View Solution100 surnames were randomly picked up for a test and fequency distribution of the number of letters in the English alphabet in the surnames was found as follows :

Draw a histogram to depict the given informationView Solution100 surnames were randomly picked up for a test and fequency distribution of the number of letters in the English alphabet in the surnames was found as follows :

Write the class interval in which the maximum number of surnames lie.View Solution100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letter in English alphabet in the surnames was found as follows:
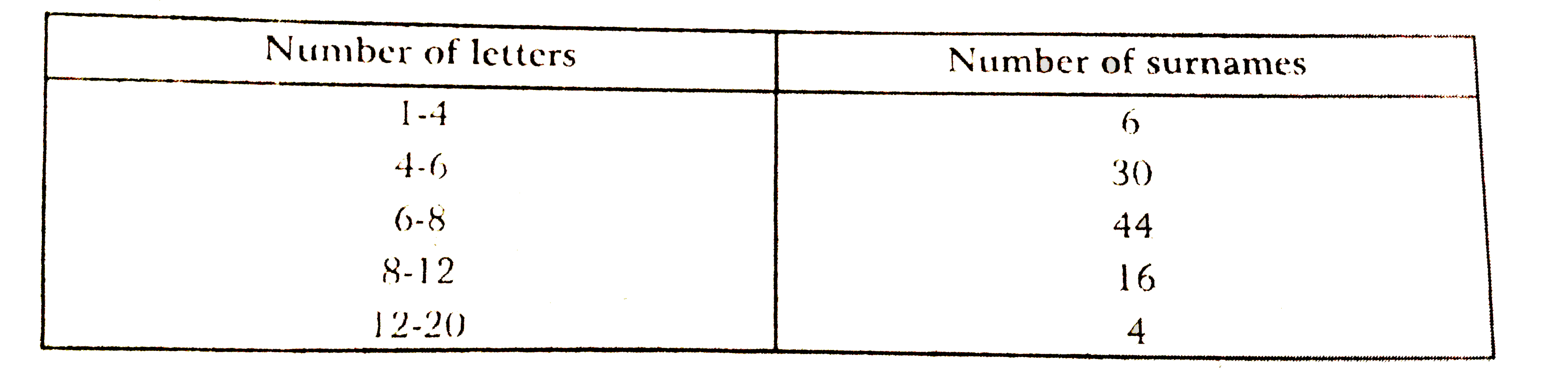
(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.View SolutionRead the following text and answer the following question on the basis of the same.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
Determine the median number of letters in the surnames.View SolutionRead the following text and answer the following question on the basis of the same.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
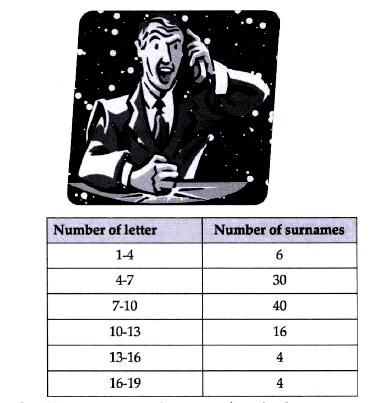
Cumulative frequency of modian class:View Solution

