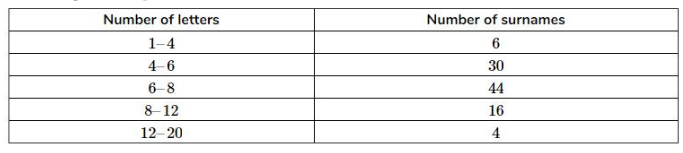
100 surnames were randomly picked up from a telephone directely and the distribution of the number of letters of the English alphabet in the surnames are obtained as follows
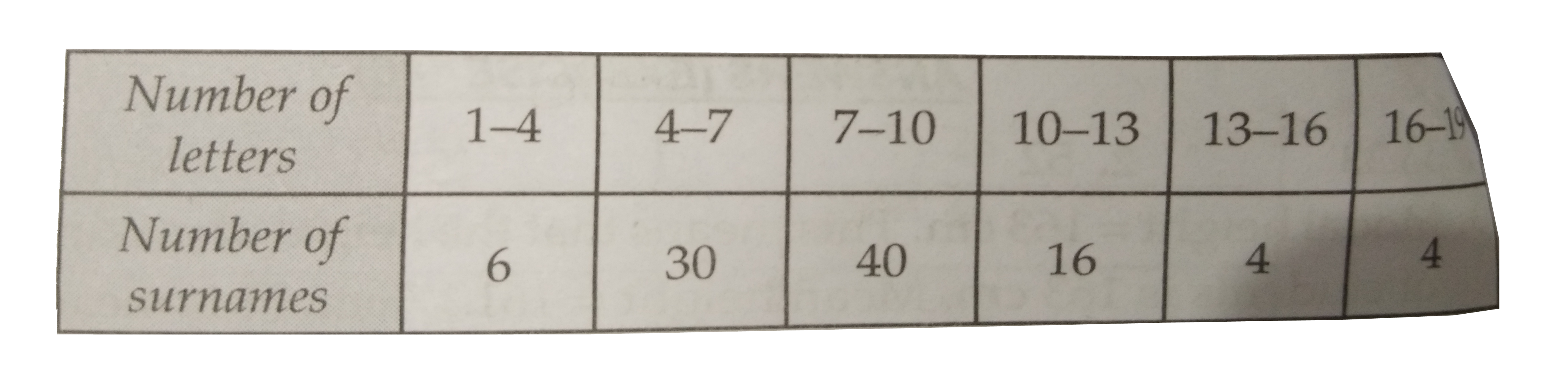
Determine the median and mean number of letters in the surnames .
Also, find the modal size of surnames
We have

Clearly , A=11.5,h=3,Σfi=100andΣ(fiui)=−106
Mean , ¯x=A+{h×Σ(fIui)Σfi}=11.5+{3×(−106)100}
=11.5-3.18=8.32
Here N=100 ⇒N2=50
Cumulative frequency just greater than 50 is 76 and the corresponding class is 7-10 . Thus , the median class =36 N2=50
Median,Me=l+⎧⎪
⎪⎨⎪
⎪⎩h×(N2−cf)f⎫⎪
⎪⎬⎪
⎪⎭
=7+{3×(50−36)40}=7+(3×1440)
7+2120=7+1.05=8.05
Mode =3(median)-2(mean)
=3×8.05−2×8.32=24.15−16.64=7.51
Topper's Solved these Questions
- MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - Exercise 18A
2 Videos
- MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - EXERCISE 18 A
25 Videos
- MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - SOLVED EXAMPLES
18 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
- PERIMETER AND AREA OF PLANE FIGURES BOOK - RS AGGARWALCHAPTER - PERIMETER AND AREA OF PLANE FIGURES EXERCISE - TEST YOURSELF (SHORT -ANSWER QUESTIONS)
1 Videos
Similar Questions
100 surnames ware randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows :
Determine the median number of letters in the surnames.

View Solution100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.

View SolutionRead the following text and answer the following question on the basis of the same.
100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
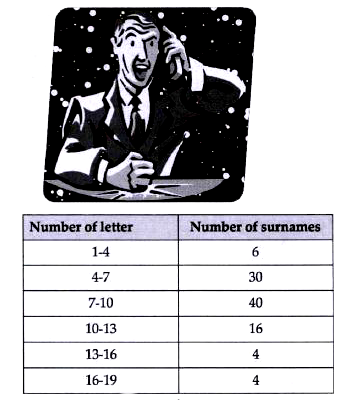
Determine the median number of letters in the surnames.
View Solution100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Sum of lower limit of median and modal class is:
View Solution100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
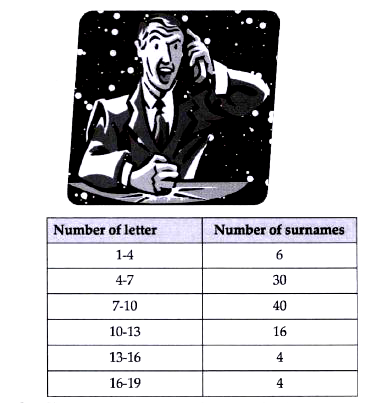
What is the upper limit of modal class?
View Solution100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
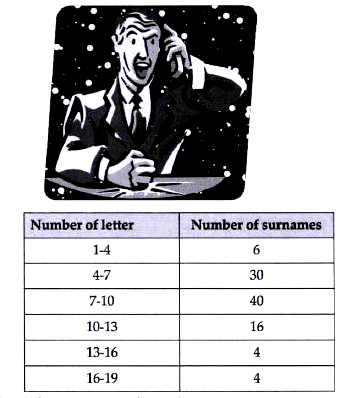
What is the upper limit of median class?
View Solution101 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

Write the class interval in which the maximum number of surnames lie.
View Solution100 surnames were randomly picked up for a test and fequency distribution of the number of letters in the English alphabet in the surnames was found as follows :

Draw a histogram to depict the given information
View Solution100 surnames were randomly picked up for a test and fequency distribution of the number of letters in the English alphabet in the surnames was found as follows :

Write the class interval in which the maximum number of surnames lie.
View Solution100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:
(i) Draw a histogram
(ii) write the class interval in which maximum number of surnames lie .
View Solution
