2n players of equal strength are playing a knock out tournament. If they are paired at randomly in all rounds, find out the probability that out of two particular players S1andS2, exactly one will reach in semi-final (n∈N,n≥2).Solution in Bengali
Four players will reach in semi-final.
Since all the players are of equal strength, this is equivalent to selecting four players out of 2n players.
Total number of ways = .2nC4
Favorable number of ways = Selecting 4 players from 2n players of which 3 players are from (2n−2) players (other than S1 and S2) and 1 from S1 and S2
∴ Required probability = .(2n−2)C3×2.2nC4
=(2n−2)×(2n−3)×(2n−4)×82n(2n−1)(2n−2)(2n−3)
=8×(2n−4)2n(2n−1)
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Solved Example
9 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
When a fair dice is rolled, the number that comes up top is a number between one to six. Assuming we roll the dice once, to check the possibility of three coming up.
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
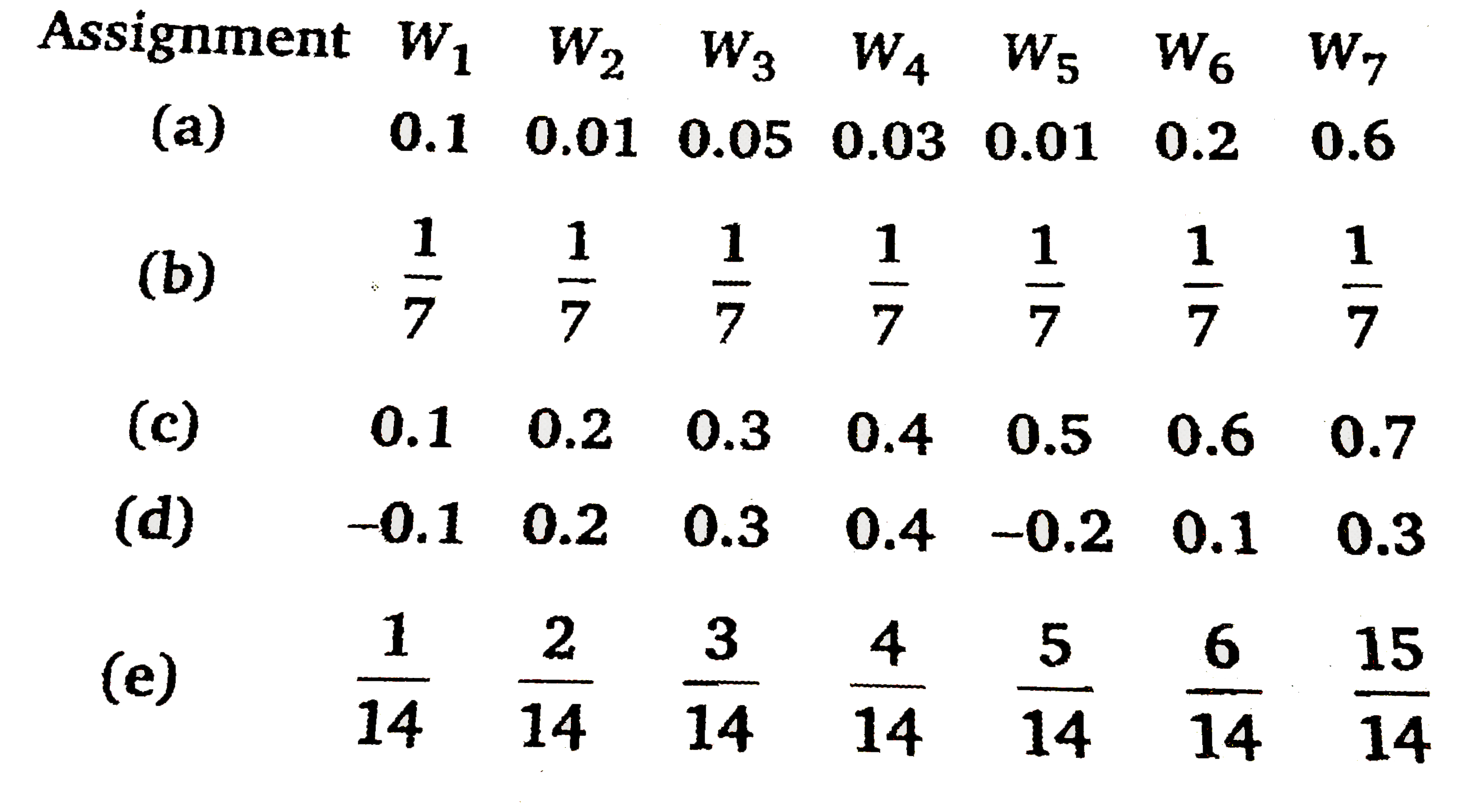
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View Solution2n players of equal strength are playing a knock out tournament. If they are paired at randomly in all rounds, find out the probability that out of two particular players S1andS2, exactly one will reach in semi-final (n∈N,n≥2).
View SolutionIn a knockout tournament 2^n equally skilled players; S_1.S_2.......S_(2^n)are participating. In each roundplayers are divided in pair at random and winner from each pair moves in the next round. If S_2 reaches thesemifinal then the probability that S_1 wins the tournament is 1/20. Find the value of 'n'.
View SolutionSixteen players S1,S2,…,S16 play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players decided to the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.
(a) Find the prabability that the player S1 is among the eight winners.
(b) Find the probability that exactly one of the two players S1andS2 is among the eight winners.
View Solution8 players P1,P2,P3,…,P8 play a knock out tournament. It is known that all the players are of equal strength. The tournament is held in three rounds where the players are paired at random in each round. If it is given that P1 wins in the third round. If p be the probability that P2 loses in second round, then the value of 7p is
View Solution8n players P_(1),P_(2),P_(3)……..P_(8n) play a knock out tournament. It is known that all the players are of equal strength. The tournament is held in 3 where the players are paired at random in each round. If it is given that P_(1) wins in the third round. Find the probability that P_(2) looses in the second round.
View Solution2n players of equal strength are playing a knock out tournament. If they are paired at randomly in all rounds, find out the probability that out of two particular players S1andS2, exactly one will reach in semi-final (n∈N,n≥2).
View SolutionEight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?
View Solution2n players of equal strength are playing a knock out tournament. If they are paired at randomly in all rounds, find out the probability that out of two particular players S1andS2, exactly one will reach in semi-final (n∈N,n≥2).
View SolutionIn a knockout tournament 2n equally skilled players, S1,S2,….S2n, are participatingl. In each round, players are divided in pair at random and winner from each pair moves in the next round. If S2 reaches the semi-final, then the probability that S1 wins the tournament is 1/84. The value of n equals _______.
View Solution8n players P_1, P_2, P_3, ,P_(8n) play a knock out tournament. It is known that all the players are of equal strength. The tournament is held in three rounds where the players are paired at random in each round. If it is given that P_1 Wins in the third round .Find the probability of P_2 loses in the second round.
View Solution2n players of equal strength are playing a knock out tournament. If they are paired at randomly in all rounds, find out the probability that out of two particular players S1andS2, exactly one will reach in semi-final (n∈N,n≥2).
View SolutionEight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?
View Solution
