2x−y+4=0 is a diameter of a circle which circumscribes a rectangle ABCD. If the coordinates of A, B are (4, 6) and (1, 9) respectively, find the area of this rectangle ABCD.
The correct Answer is:A
To solve the problem step by step, we will follow these steps:
Step 1: Find the midpoint of line segment AB
The coordinates of points A and B are given as A(4, 6) and B(1, 9). The midpoint L of AB can be calculated using the midpoint formula:
L=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
L=(4+12,6+92)=(52,152)
Step 2: Find the slope of line segment AB
The slope m of line segment AB can be calculated using the formula:
m=y2−y1x2−x1
Substituting the coordinates of A and B:
m=9−61−4=3−3=−1
Step 3: Find the slope of line OL
Since OL is perpendicular to AB, the slope of OL will be the negative reciprocal of the slope of AB:
slope of OL=1
Step 4: Write the equation of line OL
Using the point-slope form of the equation of a line y−y1=m(x−x1):
y−152=1(x−52)
Simplifying this, we get:
y−152=x−52
y=x+5
Step 5: Find the intersection of line OL and the diameter
The diameter of the circle is given by the equation 2x−y+4=0. We can rewrite this as:
y=2x+4
Now, we set the equations of OL and the diameter equal to find the intersection point:
x+5=2x+4
Solving for x:
5−4=2x−x⟹1=x⟹x=1
Substituting x=1 back into the equation of OL to find y:
y=1+5=6
Thus, the center O of the circle is at the coordinates O(1,6).
Step 6: Calculate the distance OL
Now we will find the distance OL using the distance formula:
OL=√(xL−xO)2+(yL−yO)2
Substituting the coordinates of L and O:
OL=√(52−1)2+(152−6)2
=√(32)2+(32)2
=√94+94=√184=√92=3√2
Step 7: Calculate the length of rectangle ABCD
Since OL is half the length of the rectangle, the full length AD is:
AD=2×OL=2×3√2=6√2=3√2
Step 8: Calculate the length AB
Using the distance formula for AB:
AB=√(1−4)2+(9−6)2=√(−3)2+(3)2=√9+9=√18=3√2
Step 9: Calculate the area of rectangle ABCD
The area A of rectangle ABCD is given by:
A=AB×AD=(3√2)×(3√2)=9×2=18
Thus, the area of rectangle ABCD is 18.
---
The coordinates of points A and B are given as A(4, 6) and B(1, 9). The midpoint L of AB can be calculated using the midpoint formula:
The slope m of line segment AB can be calculated using the formula:
Since OL is perpendicular to AB, the slope of OL will be the negative reciprocal of the slope of AB:
Using the point-slope form of the equation of a line y−y1=m(x−x1):
y=x+5
The diameter of the circle is given by the equation 2x−y+4=0. We can rewrite this as:
Now we will find the distance OL using the distance formula:
=√(32)2+(32)2
=√94+94=√184=√92=3√2
Since OL is half the length of the rectangle, the full length AD is:
Using the distance formula for AB:
The area A of rectangle ABCD is given by:
Topper's Solved these Questions
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
16 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- COMPLEX NUMBERSBOOK - ARIHANT MATHS ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Complex Number Exercise 8
2 Videos
Similar Questions
One of the diameter of a circle circumscribing the rectangle ABCD is 4y=x+7, If A and B are the points (−3,4) and (5,4) respectively, then the area of rectangle is
View SolutionOne of the diameters of the circle circumscribing the rectangle ABCD is 4y=x+y. If AandB are the points (−3,4)and(5,4) respectively, find the area of the rectangle and equation of the circle.
View Solution
Knowledge Check
In the figure, the area of parallelograms EBFD and AECF are 3 and 2, respectively. What is the area of rectangle ABCD?
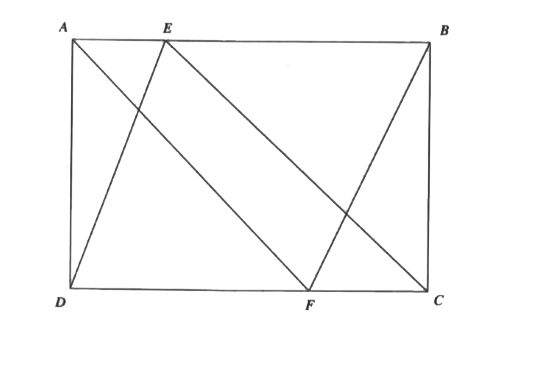 A3B4C5D4√3
A3B4C5D4√3
Column I|Column II The length of the common chord of two circles of radii 3 units and 4 units which intersect orthogonally is k5 . Then k is equal to|p. 1 The circumference of the circle x2+y2+4x+12y+p=0 is bisected by the circle x2+y2−2x+8y−q=0. Then p+q is equal to|q. 24 The number of distinct chords of the circle 2x(x−√2)+y(2y−1)=0 , where the chords are passing through the point (√2,12) and are bisected on the x-axis, is|r. 32 One of the diameters of the circle circumscribing the rectangle ABCD is 4y=x+7. If AandB are the poinst (−3,4) and (5, 4), respectively, then the area of the rectangle is|s. 36
View SolutionABCD is a parallelogram. If the coordinates of A, B, C are (2,3), (1,4)and (0,−2) respectively, find the coordinates of D.
View SolutionOne of the diameters of circle circumscribing the rectangle ABCD is4y=x+7. If A and B are the points (−3,4) and (5,4) respectively and area of rectangle is p then p4 is equal to
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Then, the area of the rectangle is
View SolutionA square has the same area as that of a rectangle. The length and the breadth of the rectangle are 9cm and 4cm, respectively.
Find the area of the rectangle.
View SolutionA rectangle ABCD is inscribed in a circle with a diameter lying along the line 3y=x+10. If A and B are the points (−6,7)and(4,7) respectively, find the area of the rectangle and equation of the circle.
View SolutionThe sides of a rectangle are x and y, respectively. Find the rule for finding the perimeter of the rectangle.
View Solution
