55,34,48,38,70,44,54,46,63,42.
Find the mean deviation about the median.
To find the mean deviation about the median for the given data set, we will follow these steps:
Step 1: Organize the Data
First, we need to arrange the data in ascending order.
Data: 55, 34, 48, 38, 70, 44, 54, 46, 63, 42
Ascending Order: 34, 38, 42, 44, 46, 48, 54, 55, 63, 70
Step 2: Find the Median
Since there are 10 observations (an even number), the median is calculated as the average of the 5th and 6th terms in the ordered list.
5th term: 46
6th term: 48
Median (M):
M=46+482=942=47
Step 3: Calculate the Absolute Deviations
Next, we will calculate the absolute deviations from the median for each data point.
Absolute Deviations:
- |34 - 47| = 13
- |38 - 47| = 9
- |42 - 47| = 5
- |44 - 47| = 3
- |46 - 47| = 1
- |48 - 47| = 1
- |54 - 47| = 7
- |55 - 47| = 8
- |63 - 47| = 16
- |70 - 47| = 23
Step 4: Sum of Absolute Deviations
Now, we will sum all the absolute deviations calculated in the previous step.
Sum of Absolute Deviations:
13+9+5+3+1+1+7+8+16+23=86
Step 5: Calculate the Mean Deviation
Finally, we will calculate the mean deviation by dividing the sum of absolute deviations by the number of observations (n).
Mean Deviation (MD):
MD=Sum of Absolute Deviationsn=8610=8.6
Final Answer
The mean deviation about the median is 8.6.
---
First, we need to arrange the data in ascending order.
Since there are 10 observations (an even number), the median is calculated as the average of the 5th and 6th terms in the ordered list.
6th term: 48
M=46+482=942=47
Next, we will calculate the absolute deviations from the median for each data point.
- |34 - 47| = 13
- |38 - 47| = 9
- |42 - 47| = 5
- |44 - 47| = 3
- |46 - 47| = 1
- |48 - 47| = 1
- |54 - 47| = 7
- |55 - 47| = 8
- |63 - 47| = 16
- |70 - 47| = 23
Now, we will sum all the absolute deviations calculated in the previous step.
13+9+5+3+1+1+7+8+16+23=86
Finally, we will calculate the mean deviation by dividing the sum of absolute deviations by the number of observations (n).
MD=Sum of Absolute Deviationsn=8610=8.6
The mean deviation about the median is 8.6.
Topper's Solved these Questions
- STATISTICSBOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Frequently Asked Questions
4 Videos
- STATISTICSBOOK - MODERN PUBLICATIONCHAPTER - STATISTICSEXERCISE - Exercise 15(a) (Long Answer Type Questions- I)
6 Videos
- SETS BOOK - MODERN PUBLICATIONCHAPTER - SETS EXERCISE - CHAPTER TEST 1
12 Videos
- STRAIGHT LINES BOOK - MODERN PUBLICATIONCHAPTER - STRAIGHT LINES EXERCISE - Chapter test
12 Videos
Similar Questions
The scores of a batsman in ten innings are : 38,70,48,34,42,55,63,46,54,44. Find the mean deviation about the median.
View SolutionThe scores of a batsman in ten innings are : 38,70,48,34,42,55,63,46,54,44. Find the mean deviation about the median.
View SolutionFind the mean deviation about the mean of the distributon .

View SolutionFind the mean deviation about the mean of the distributon .

View SolutionFind the mean deviation using median:
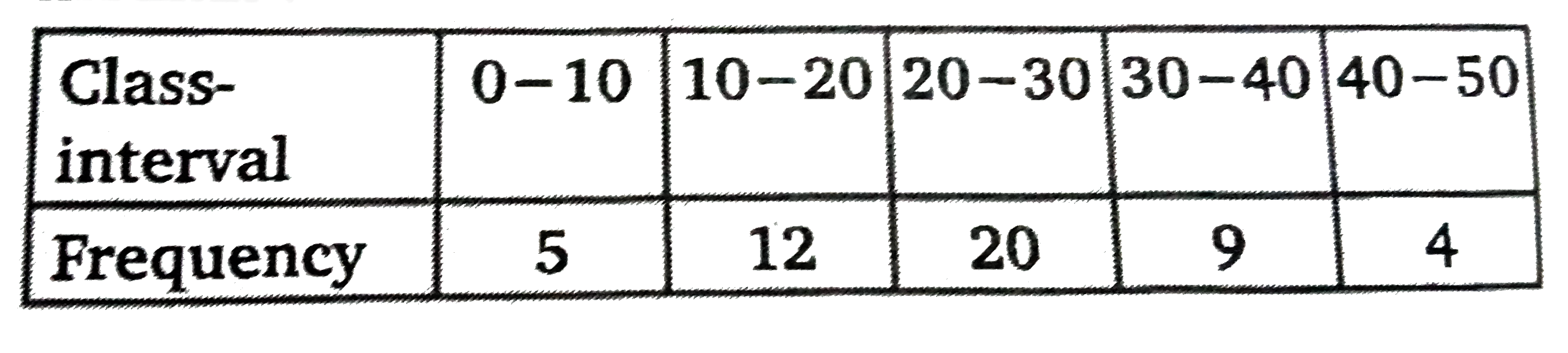
View SolutionFind the mean deviation about the median for the data in Question

View SolutionFind the mean deviation about the median for the data in Question
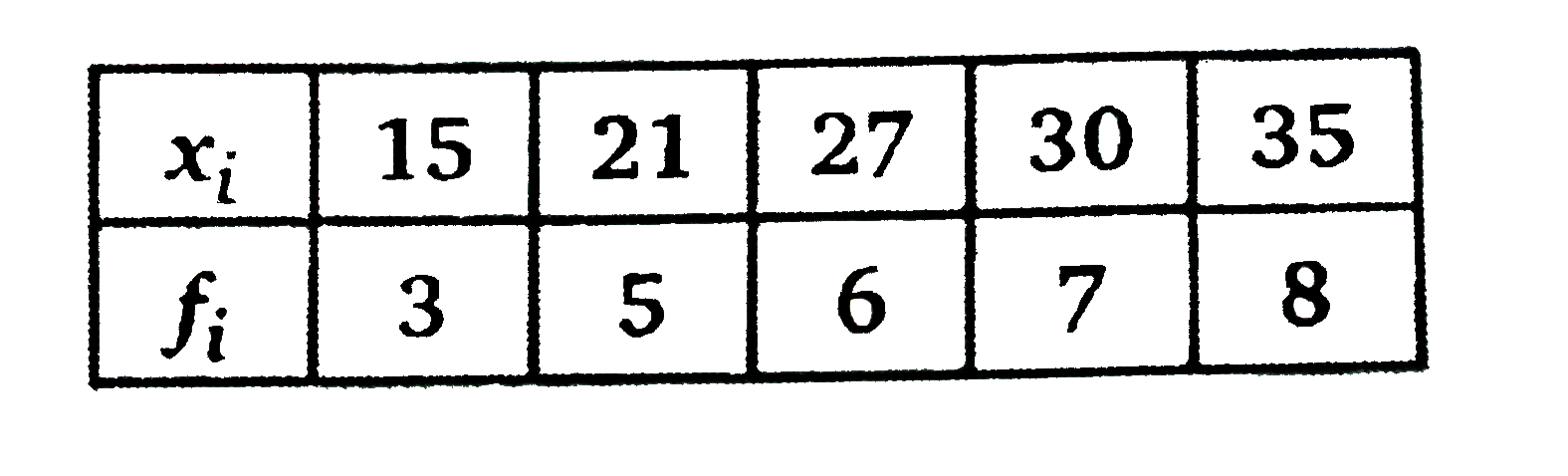
View SolutionFind the mean deviation about the median for the following data:
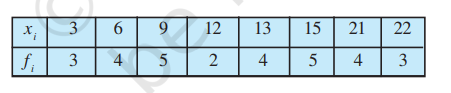
View SolutionFind the mean deviation about the mean for the following data.

View SolutionFind the mean deviation about the mean for the data in Question:

View Solution
