80 coins are placed in a st. line on the ground. The distance between any two consecutive coins is 10 metres. How far must a person travel to bring them one by one to a basket placed 10 metres behind the first coin?
To solve the problem step by step, let's break down the situation and calculate the total distance the person must travel to bring all 80 coins to the basket.
Step 1: Understand the Setup
- There are 80 coins placed in a straight line.
- The distance between any two consecutive coins is 10 meters.
- The basket is placed 10 meters behind the first coin.
Step 2: Calculate the Position of Each Coin
- The position of the first coin is at 0 meters.
- The position of the second coin is at 10 meters.
- The position of the third coin is at 20 meters.
- Continuing this way, the position of the nth coin can be calculated as:
Position of the nth coin=10×(n−1) meters
- For the 80th coin:
Position of the 80th coin=10×(80−1)=10×79=790 meters
Step 3: Calculate the Distance Traveled for Each Coin
- To pick up the first coin, the person travels 10 meters to the coin and 10 meters back to the basket:
Distance for 1st coin=10+10=20 meters
- For the second coin, the person travels 20 meters to the coin and 20 meters back to the basket:
Distance for 2nd coin=20+20=40 meters
- For the third coin, the distance is:
Distance for 3rd coin=30+30=60 meters
- Continuing this way, the distance for the nth coin is:
Distance for nth coin=(10n)+(10n)=20n meters
Step 4: Total Distance Traveled for All Coins
- The total distance traveled to bring all 80 coins can be calculated as the sum of the distances for each coin:
Total Distance=20(1+2+3+...+80)
- The sum of the first n natural numbers is given by:
Sn=n(n+1)2
- For n = 80:
S80=80×812=3240
- Therefore, the total distance is:
Total Distance=20×3240=64800 meters
Step 5: Convert to Kilometers
- To convert meters to kilometers:
64800 meters=648001000=64.8 kilometers
Final Answer
The total distance the person must travel to bring all 80 coins to the basket is 64.8 kilometers.
---
- There are 80 coins placed in a straight line.
- The distance between any two consecutive coins is 10 meters.
- The basket is placed 10 meters behind the first coin.
- The position of the first coin is at 0 meters.
- The position of the second coin is at 10 meters.
- The position of the third coin is at 20 meters.
- Continuing this way, the position of the nth coin can be calculated as:
Position of the nth coin=10×(n−1) meters
- For the 80th coin:
Position of the 80th coin=10×(80−1)=10×79=790 meters
- To pick up the first coin, the person travels 10 meters to the coin and 10 meters back to the basket:
Distance for 1st coin=10+10=20 meters
- For the second coin, the person travels 20 meters to the coin and 20 meters back to the basket:
Distance for 2nd coin=20+20=40 meters
- For the third coin, the distance is:
Distance for 3rd coin=30+30=60 meters
- Continuing this way, the distance for the nth coin is:
Distance for nth coin=(10n)+(10n)=20n meters
- The total distance traveled to bring all 80 coins can be calculated as the sum of the distances for each coin:
Total Distance=20(1+2+3+...+80)
- The sum of the first n natural numbers is given by:
Sn=n(n+1)2
- For n = 80:
S80=80×812=3240
- Therefore, the total distance is:
Total Distance=20×3240=64800 meters
- To convert meters to kilometers:
64800 meters=648001000=64.8 kilometers
The total distance the person must travel to bring all 80 coins to the basket is 64.8 kilometers.
Topper's Solved these Questions
- SEQUENCE AND SERIES BOOK - ICSECHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE 14 (a)
13 Videos
- SEQUENCE AND SERIES BOOK - ICSECHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE 14 (b)
22 Videos
- SELF ASSESSMENT PAPER 5BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - SECTION C
11 Videos
- SEQUENCES AND SERIESBOOK - ICSECHAPTER - SEQUENCES AND SERIESEXERCISE - MULTIPLE CHOICE QUESTIONS
34 Videos
Similar Questions
Two plane mirrors are placed parallel to each other. The distance between the mirrors is 10cm. An object is placed between the mirrors at a distance of 4cm from one of them, say M1. What is the distance between the first time formed at M1 and the second image formed at M2 ?
View SolutionTwo parallel rails of a railway track insulated from each other and with the ground are connected to a millivoltmeter. The distance between the rails is one metre. A train is traveling with a velocity of 72kmph along the track. The reading of the millivoltmetre (in mV) is : (Vertical component of the earth's magnetic induction is 2×10−5T)
View SolutionIn a potato race 20 potatoes are placed in a line at intervals of 4meters with first potato 24metres from the starting point. A constant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
View SolutionIn a potato race 20 potatoes are placed in a line at intervals of 4meters with first potato 24metres from the starting point. A contestant is required to bring the potatoes back to the starting place one at a time. How far would he run in bringing back all the potatoes?
View SolutionTwo waves, each having a frequency of 100 Hz and a wavelength of 2.0 cm, are travelling in the same direction on a string. What is the phase difference between the waves (a) if the second wave was produced 0.015 s later than the first one at the same place, (b) if the two waves were produced at the same instant but the first one was produced a distance 4.0 cm behind the second one ? (c) If each of the waves has an amplitude of 2.0 mm, what would be the amplitudes of the resultant waves in part (a) and (b) ?
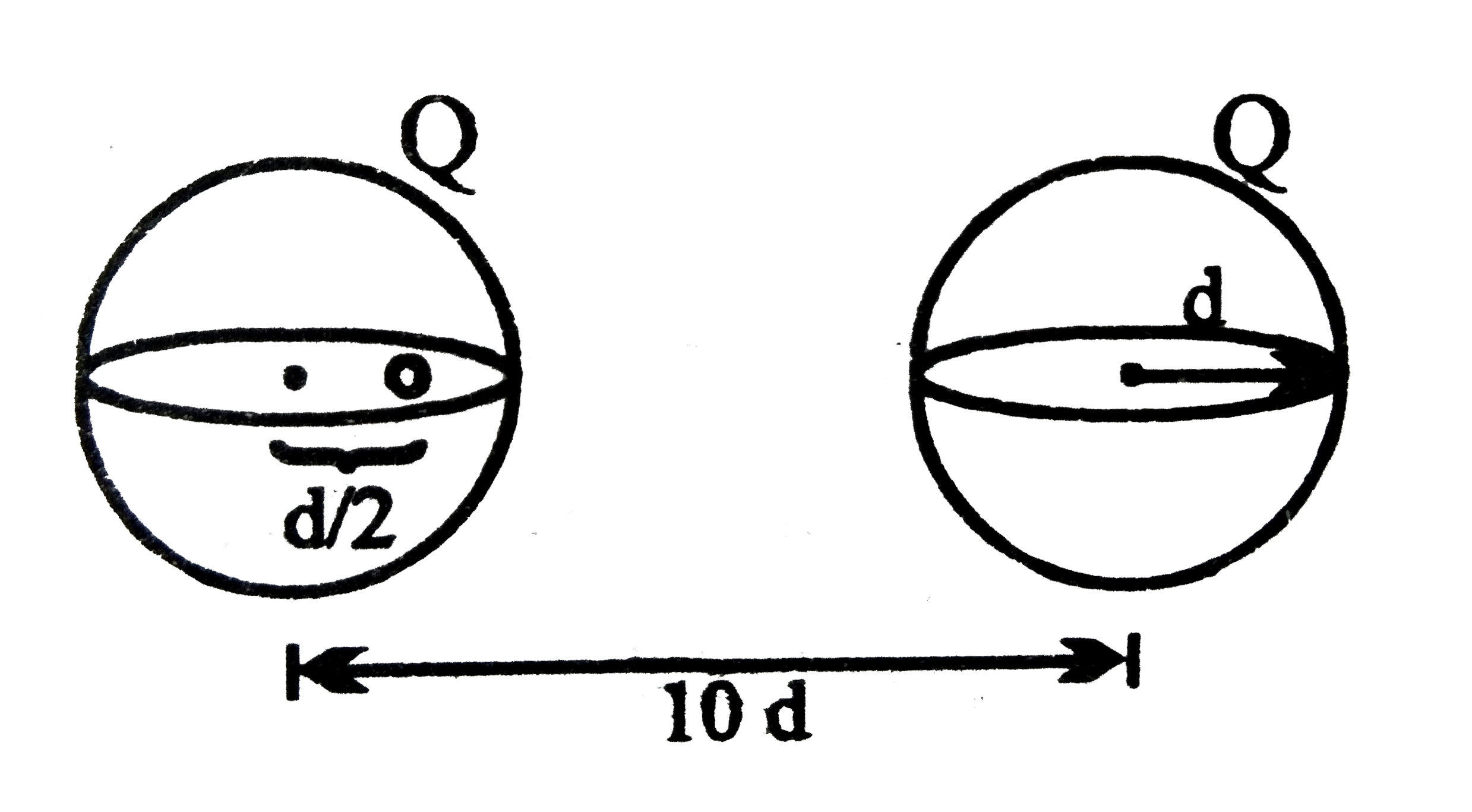
View SolutionTwo spherical , nonconducting and very tin shells of uniformly distributed positive charge Q and radius d are located a distance 10d from each other . A positive point charge q is placed inside one of the shells at a distance d/2 from the center, on the line connecting the centers of the two shells , as shown in the figure, What is the net force on the charge q ? .
View SolutionTwo cyclists,moving with equal speeds of 10 km/hr,are approaching each oher along a straight road.When the distance between them is 20 km a fly starting from cycle,keeps on flying alternatively from one cycle to the other.If the fly has a constant speed of 40 km/hr.Find the total distance travelled by the fly before the cyclists meet is.
View Solution25 trees are planted in a straight line 5 metre apart from each other. To water them the gardener must bring water for each tree separately from a well 10 metre from the first tree in line with the trees. Let d be the distance we have to cover in order to water all the trees beginning with the first if he starts from the well.Find sum of digits of d ?
View SolutionAlong a road lie an odd number of stones placed at intervals of 10 metres. These stones have to be assembled around the middle stone. A person can carry only one stone at a time. A man carried the job with one of the end stones by carrying them in succession. In carrying all the stones he covered a distance of 3 km. Find the number of stones.
View SolutionAlong a road lie an odd number of stones placed at intervals of 10 metres. These stones have to be assembled around the middle stone. A person can carry only one stone at a time. A man carried the job with one of the end stones by carrying them in succession. In carrying all the stones he covered a distance of 3 km. Find the number of stones.
View Solution
