A and B are fixed points such that AB=2a. The vertex C of ΔABC moves such that cotA+cotB= constant. The locus of C is a
perpendicular to AB
parallel to AB
inclined at an angle A-B to AB
none of these
The correct Answer is:B
We have,
cotA=ADCDandcotB=DBCD
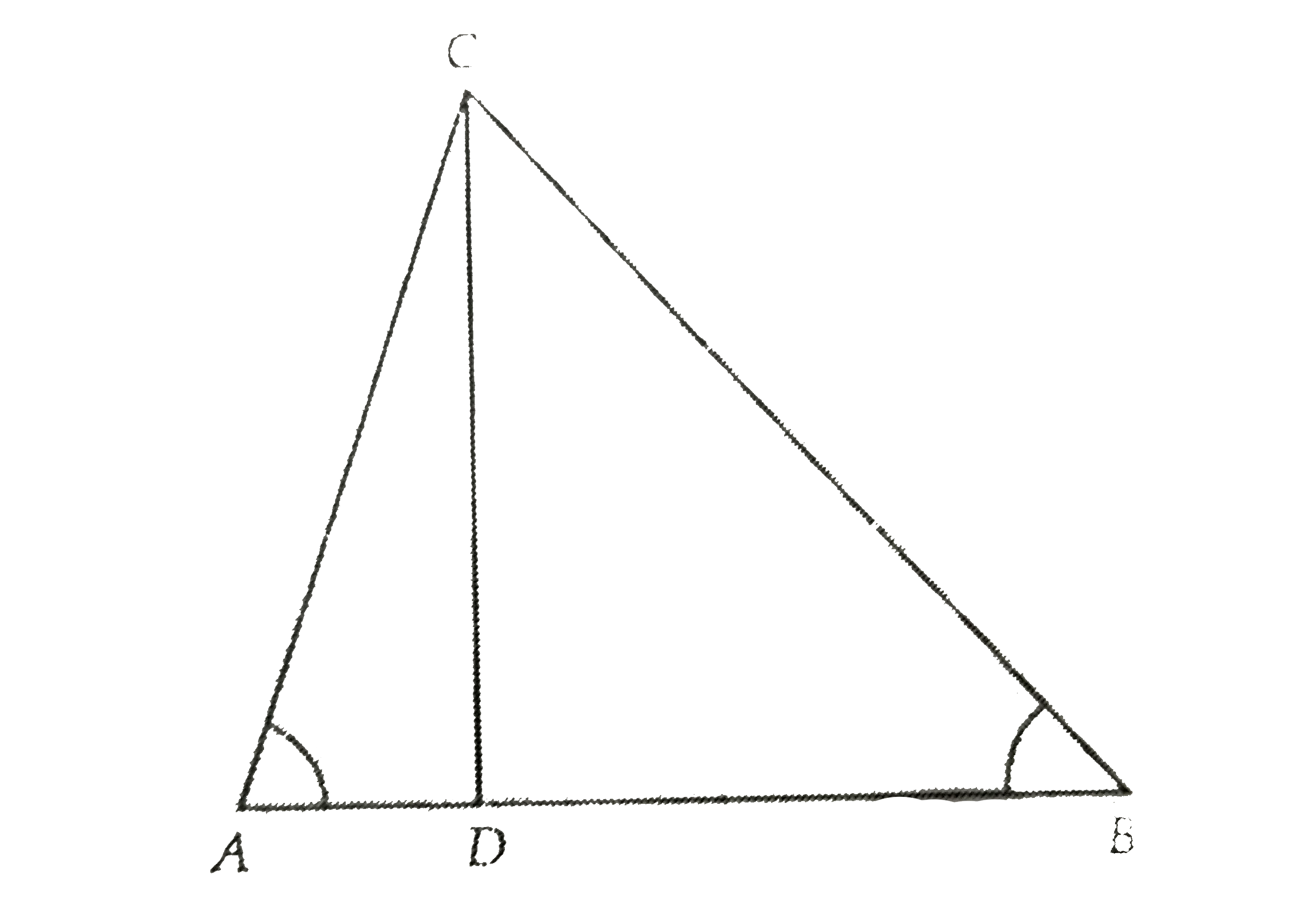
⇒cotA+cotB=AD+DBCD
⇒ Constant=ABCD
⇒CD= constant
⇒ Locus of C is a striaght line parallel to AB.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Section-1 Solved MCQs (Example)
1 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION - II (ASSERTION - REASON TYPE MCQs)
14 Videos
- STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ILLUSTRATION 18
1 Videos
- SETSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - SETSEXERCISE - Chapter Test
30 Videos
Similar Questions
A and B are fixed points such that AB=2a. The vertex C of ΔABC such that cotA+cotB=constant. Then locus of C is
View SolutionA & B are two fixed points. The vertex C of △ABC moves such that cotA+cotB= constant. The locus of C is a straight line
View SolutionIn a ΔABC, prove that:
2r≤acotA+bcotB+ccotC3≤R
View SolutionProve that :
cotA+tanBcotB+tanA=cotAtanB
View SolutionIf A+B+C=π, prove that: cot2A+cot2B+cot2C≥1
View SolutionThe base AB of a triangle is fixed and its vertex C moves such that sin A =k sin B (k≠1). Show that the locus of C is a circle whose centre lies on the line AB and whose radius is equal to ak(1−k2), a being the length of the base AB.
View SolutionBase BC of triangle ABC is fixed and opposite vertex A moves in such a way that tan.B2tan.C2 is constant. Prove that locus of vertex A is ellipse.
View SolutionA triangle ABC with fixed base BC , the vertex A moves such that cosB+cosC=4sin2A2. If a,bandc, denote the length of the sides of the triangle opposite to the angles A,B,andC , respectively, then (a)b+c=4a (b) b+c=2a (c)the locus of point A is an ellipse (d)the locus of point A is a pair of straight lines
View SolutionIn a triangle ABC with fixed base BC, the vertex A moves such that cosB+cosC=4sin2A/2
If a, b and c denote the lengths of the sides of the triangle opposite to the angles A,B and C respectively, then
View SolutionIn any ΔABC, prove that (a+b−c)cot(B2)=(a−b+c)cot(C2)
View Solution
