A, B, C, D and E are coplanar points and three of them lie in a straight line. What is the maximum number of triangles that can be drawn with these points as their vertices ?
5
9
10
12
The correct Answer is:B
To determine the maximum number of triangles that can be formed using the points A, B, C, D, and E, where three of them are collinear, we can follow these steps:
Step 1: Understand the Points Configuration
We have 5 points: A, B, C, D, and E. Among these, let's assume points A, B, and C are collinear (lie on the same straight line).
Step 2: Calculate Total Combinations of Points
To form a triangle, we need to select 3 points from the 5 points. The total number of ways to choose 3 points from 5 is given by the combination formula:
Total combinations=(53)=5!3!(5−3)!=5×42×1=10
Step 3: Exclude Collinear Points
However, since points A, B, and C are collinear, they cannot form a triangle. We need to exclude this combination from our total:
Collinear combination=(33)=1
Step 4: Calculate Valid Triangles
Now, we subtract the collinear combination from the total combinations:
Valid triangles=Total combinations−Collinear combination=10−1=9
Conclusion
Thus, the maximum number of triangles that can be formed with the points A, B, C, D, and E, where A, B, and C are collinear, is 9.
---
We have 5 points: A, B, C, D, and E. Among these, let's assume points A, B, and C are collinear (lie on the same straight line).
To form a triangle, we need to select 3 points from the 5 points. The total number of ways to choose 3 points from 5 is given by the combination formula:
Total combinations=(53)=5!3!(5−3)!=5×42×1=10
However, since points A, B, and C are collinear, they cannot form a triangle. We need to exclude this combination from our total:
Collinear combination=(33)=1
Now, we subtract the collinear combination from the total combinations:
Valid triangles=Total combinations−Collinear combination=10−1=9
Thus, the maximum number of triangles that can be formed with the points A, B, C, D, and E, where A, B, and C are collinear, is 9.
Topper's Solved these Questions
Similar Questions
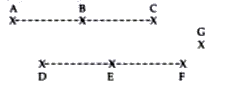
How many maximum numbers of triangles can be formed with the seven points A, B, C, D, E, F, and G ?
View SolutionTwo straight lines intersect at a point O. Points A1,A2...,An are taken on one line and points B,B2,...,Bn, on the other. If the point O is not to be used, then the number of triangles that can be drawn using these points as vertices, is
View Solution
Knowledge Check
There are p coplanar parallel lines. If any 3 points are taken on each of the lines, the maximum number of triangles with vertices at these points is:
A3pC3−pB9P2(p−1)2C4P2(P−1)D18PC2+27PC3There are 10 points in a plane. No three of these points are in a straight line. What is the total number of straight lines which can be formed by joining the points?
A90B45C40D30Answer these questions based on the following informations
Two parallel lines each have a number of distinct points marked on them. On one line there are two points P and Q. On the other line there are eight points
Find the maximum number of different triangles which could be formed having three of the ten points as their verticesA3B2C64D6
There are 10 points on a straight line AB and 8 on another straight line AC, none of them being A. How many triangles can be formed with these points as vertices?
View SolutionThere are 10 points in a plane out of which 5 are collinear. The number of straight lines than can be drawn by joining these points will be
View Solution4 points out of 11 points in a plane are collinear. Number of different triangles that can be drawn by joining them, is
View SolutionThere are 15 points in a plane, no three of which are in a straight line except 4, all of which are in a straight line. The number of triangles that can be formed by using these 15 points is:
View SolutionThere are 15 points in a plane, no two of which are in a straight line except 4, all of which are in a straight line. The number of triangles that can be formed by using these 15 points is
View Solution
