ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC=35∘ , then ∠ABC= 70∘ (b) 110∘ (c) 90∘ (d) 120∘
Given: ABCD is a parallelogram in which ∠BAC=35∘
Solution : AC is a bisector of angle BAD
So, ∠A=2∠BAC
∠A=2×35∘
∠A=70∘
Now, ∠A+∠B=180∘
( supplementary angles)
70∘+∠B=180∘
∠B=110∘
Hence, option(b) is correct.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC=35∘ , then ∠ABC= 70∘ (b) 110∘ (c) 90∘ (d) 120∘
View SolutionABCD is a parallelogram in which ∠A=70∘. Compute ∠B, ∠C and ∠D.
View SolutionABCD is a parallelogram in which ∠A=70∘ Compute ∠B, ∠C and ∠D
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
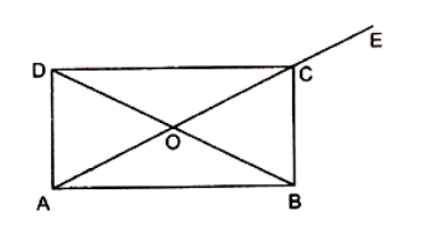 View Solution
View SolutionDiagonals of a quadrilateral ABCD bisect each other. If ∠A=45∘, then ∠B= 115∘ (b) 120∘ (c) 125∘ (d) 135∘
View SolutionThe diagonals of a parallelogram ABCD intersect at O . If ∠BOC=90∘ and ∠BDC=50∘, then ∠OAB= 40∘ (b) 50∘ (c) 10∘ (d) 900
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Find AB:AD
View SolutionABCD is a parallelogram, M is the mid-point of BD and BM bisects ∠B . Then, ∠AMB= 45∘ (b) 60∘ (c) 90∘ (d) 75∘
View SolutionIn ABC, ∠B=∠C and ray AX bisects the exterior angle ∠DAC.If ∠DAX=700, then ∠ACB= 350 (b) 900 (c) 700 (d) 550
View SolutionIn a rhombus ABCD, if ∠ACB=40∘, then ∠ADB=(a) 70∘ (b) 45∘ (c) 50∘ (d) 60∘
View Solution

