A balloon of radius r subtends an angle $α$ at the eyes of an observer and the center of balloon from the eye is $β$ . Find the height of the center of the balloon from the eye of observer .

Video Solution

Text Solution

Verified by Experts

Let O be the centre of the balloon of radius which subtends an angle $α$ at E , the eyes of observer .

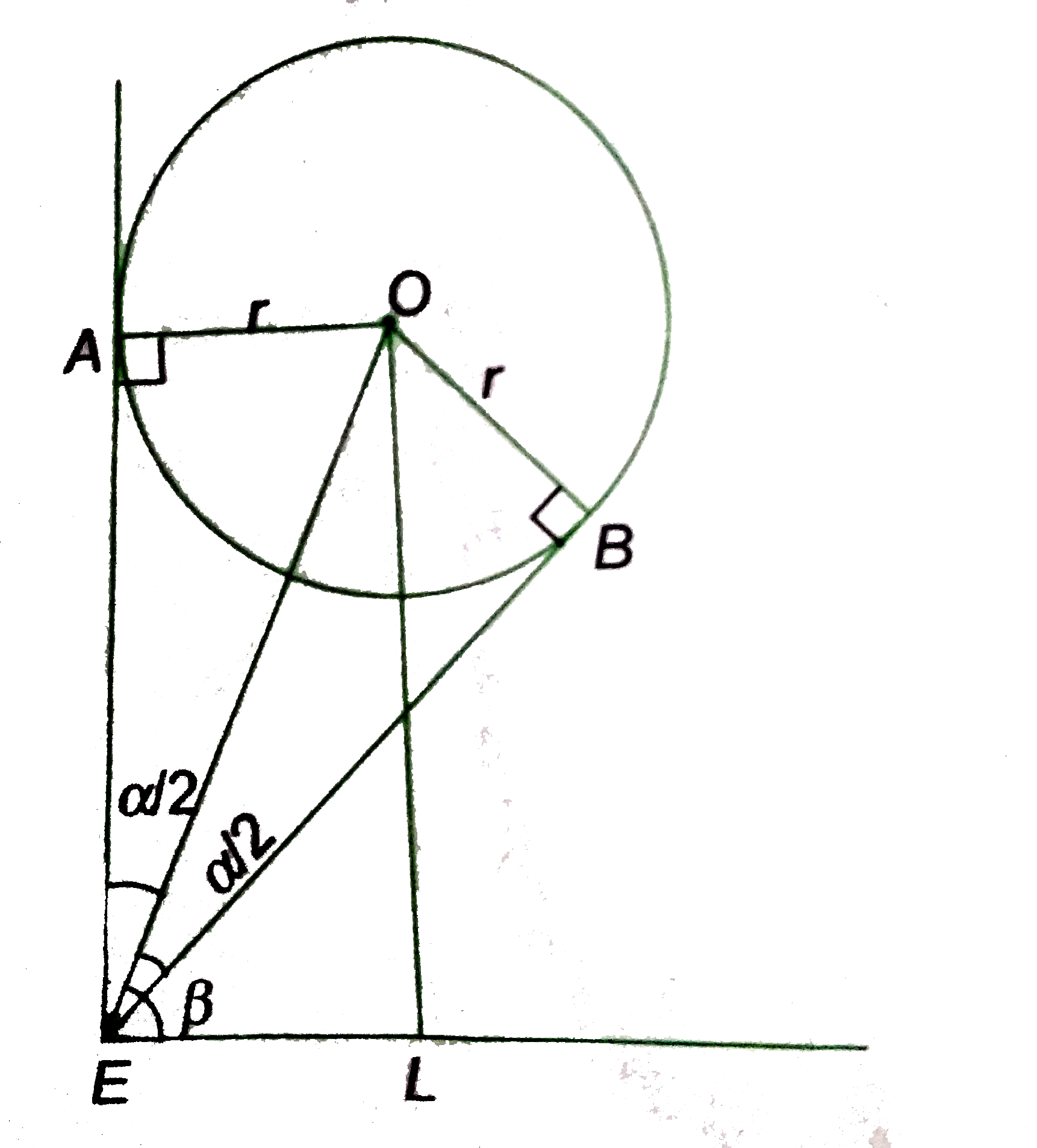
EA and EB are the tangents to the balloon .
$∴ ∠ O E A = ∠ O E B = α / 2$
Let the height OL of the balloon be h .
In $Δ$ OLE ,
h=OE sinbeta
$= r cos e c (α / 2) sin β$ ( in triangle OBE)
$= \frac{r sin β}{sin (α / 2)}$

|

Updated on:21/07/2023

Class 12 MATHS HIGHT AND DISTANCE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A round balloon of radius 'r' subtends an angle $α$ at the eye of the observer, while the angle of elevation of its centre is $β$ . Find the height of the centre of balloon.
A $r cosec (\frac{α}{2}) sin β$
B $r sin α cosec β$
C $\frac{r}{2} sin β$
D $r sec (\frac{α}{2})$
Question 2 - Select One
A round balloon of radius r subtends an angle $α$ at the eyes of the observer, while the angle of elevation of is centre is $β$ . The height of the centre of balloon is
A $r cos e c α sin \frac{β}{2}$
B $r sin α cosec \frac{β}{2}$
C $r sin \frac{α}{2} cosec β$
D $r cosec \frac{α}{2} sin β$
Question 3 - Select One
A spherical ballon of radius r subtends angle $60^{\circ}$ at the eye of an observer. If the angle of elevation of its centre is $60^{\circ}$ and h is the height of the centre of the ballon, then which one of the following is correct ?
Ah = r
Bh = $\sqrt{2}$ r
Ch = $\sqrt{3}$ r
Dh = 2r

CENGAGE-HIGHT AND DISTANCE -JEE Previous Year

Home
Ask Doubt
Profile