A balloon of radius r subtends an angleα at the eyes of an observer and the center of balloon from the eye is β . Find the height of the center of the balloon from the eye of observer . Solution in Tamil
Let O be the centre of the balloon of radius which subtends an angleα at E , the eyes of observer .
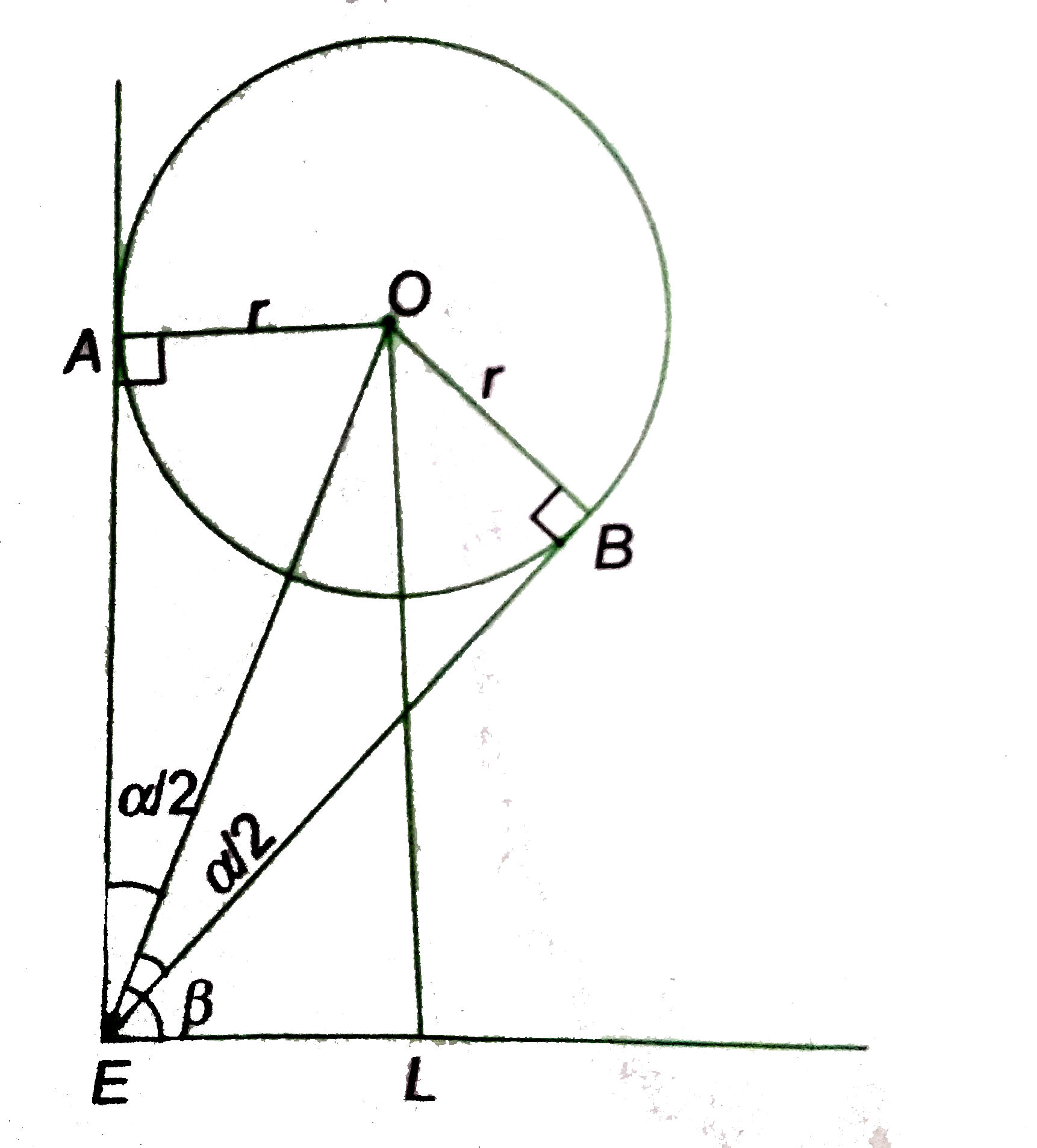
EA and EB are the tangents to the balloon .
∴∠OEA=∠OEB=α/2
Let the height OL of the balloon be h .
In Δ OLE ,
h=OE sinbeta
=rcosec(α/2)sinβ ( in triangle OBE)
=rsinβsin(α/2)
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - Exercise
18 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30o with horizontal, then the length of the wire is (a) 12 m (b) 10 m (c) 8 m (d) 6 m
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
View SolutionA round balloon of radius r subtends an angle alpha at the eye of the observer while the angle of elevation of its centre is beta Prove that the height of the centre of the balloon is r sin beta cos ec[(alpha)/(2)]
View SolutionA round balloon of radius r subtends an angle alpha at the eye of the observer while the angle of elevation of its centre is beta. Prove that the height of the centre of the balloon is r sin(beta)cos ec(alpha)/(2)
View SolutionA balloon of radius r subtends an angleα at the eyes of an observer and the center of balloon from the eye is β . Find the height of the center of the balloon from the eye of observer .
View Solutionएक गोलाकार गुब्बारा जिसकी त्रिजया r है, दर्शक की आंख पर α कोण बनाता है और इसके केन्द्र का आंख से उन्नयन कोण β हैं सिद्ध कीजिए कि गुब्बारे के केंद्र की पृथ्वी से ऊंचाई rsinβcosecα2 है।
View Solutionr त्रिज्या का एक गोल गुब्बारा प्रेक्षक की आँख पर उन्नयन कोण α बनाता है तथा इसके केंद्र का उन्नयन कोण β है| सिद्ध कीजिए की गुब्बारे के केंद्र की ऊंचाई rsinβcosecα2 है|
View SolutionA spherical balloon of radius r subtends an angle α at the eye of anb observer. If the angle of elevation of the cerntre of the balloon be β, then prove that the height of the balloon is
r cosecα2sinβ.
View Solutionr त्रिज्या वाला एक गोलाकार गुब्बारा, किसी प्रेक्षक की आँख पर कोण α करता है, जबकि इसके केन्द्रबिन्दु पर उन्नयन कोण β है । गुब्बारे के केन्द्रबिन्दु की ऊँचाई क्या है । (प्रेक्षक की ऊँचाई को नजर अन्दाज करते हुए ) ?
View SolutionA round balloon of radius 'r' subtends an angle α at the eye of the observer, while the angle of elevation of its centre is β. Find the height of the centre of balloon.
View Solutionएक r त्रिज्या का गोलीय गुब्बारा , किसी प्रेक्षक की आँख पर α कोण बनाता है। यदि गुब्बारे के केंद्र का उन्नयन कोण β हो, तो गुब्बारे के केंद्र की ऊंचाई है
View SolutionA balloon of radius r subtends an angleα at the eyes of an observer and the center of balloon from the eye is β . Find the height of the center of the balloon from the eye of observer .
View SolutionA spherical balloon of radius r subtends an angle θ at the eye of an observer. If the angle of elevation of its centre is ϕ, find the height of the centre of the balloon.

View Solution
