A body at a temperature of 500F is placed outdoors where the temperature is 1000F . If the rate of change of the temperature of a body is proportional to the temperature difference between the body and its surrounding medium. If after 5 min the temperature of the body is 600F , find (a) how long it will take the body to reach a temperature of 75 ^0 F and (b) the temperature of the body after 20 min.
Video Solution
Text Solution
Let T be the temperature of the body at time t and Tm=100 (the temperature of the surrounding medium). We have dTdt=−k(T−Tm)
dTdt+kT=kTm,
where constant of proportionally. Thus,
dTdt+kT=100k
The solution of differential equation is
T=ce−kt+100................(1)
Since T=50 when t=0
from equation (1), 50=ce−k(0)+100, or c=−50.
Sustituting this value in equation (1), we obtain
T=−50e−kt+100.....................(2)
At t=t, we are given that T=60, hence, from equation (2),
60=−50e−5k+100.
Solving for k, we obtain −40=−50e−5k or k=15ln4050
Substituting this value in equation (2), we obtain the temperature of the body at any time t as
T=−50e(1/5)In(4/5)t+100..............(3)
a) We required t when T=75. Substituting T=75 in equation (3), we have
from which we get t=15.53 min
b) We require T when t=20, Subsituting t=20 in equation (3) and then solving for T, we find
T=−50e(1/5)ln(4/5)(20)+100=79.52∘
|
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 10.1
6 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGECHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 10.2
6 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGECHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise
337 Videos
- DIFFERENTIATIONBOOK - CENGAGECHAPTER - DIFFERENTIATIONEXERCISE - Numerical Value Type
3 Videos
Similar Questions
Knowledge Check
For a small temperature difference between the body and the surroundings, the relation between the rate of heat loss R and the temperature of the body is depicted by
A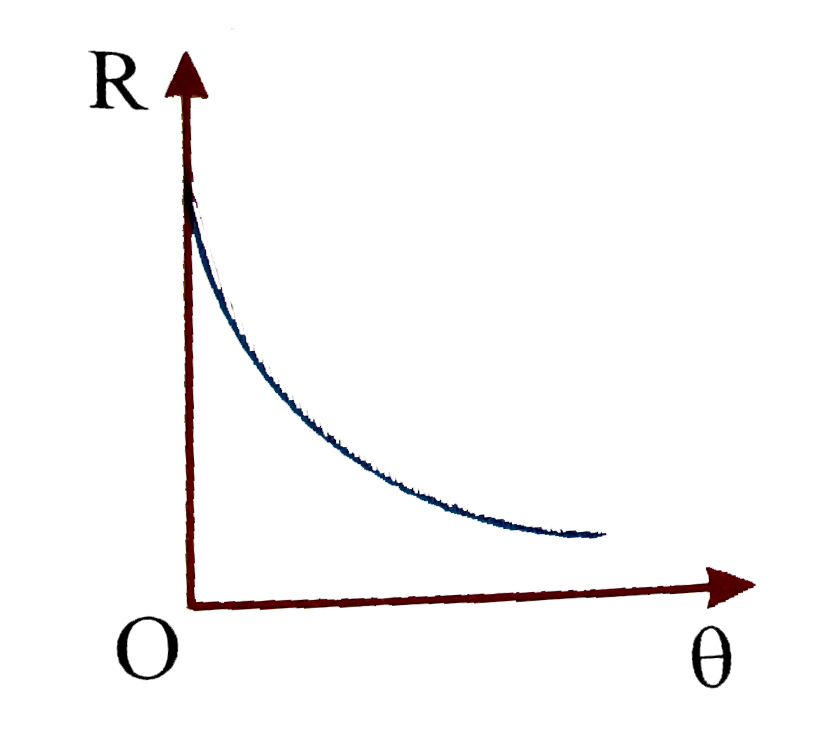 B
B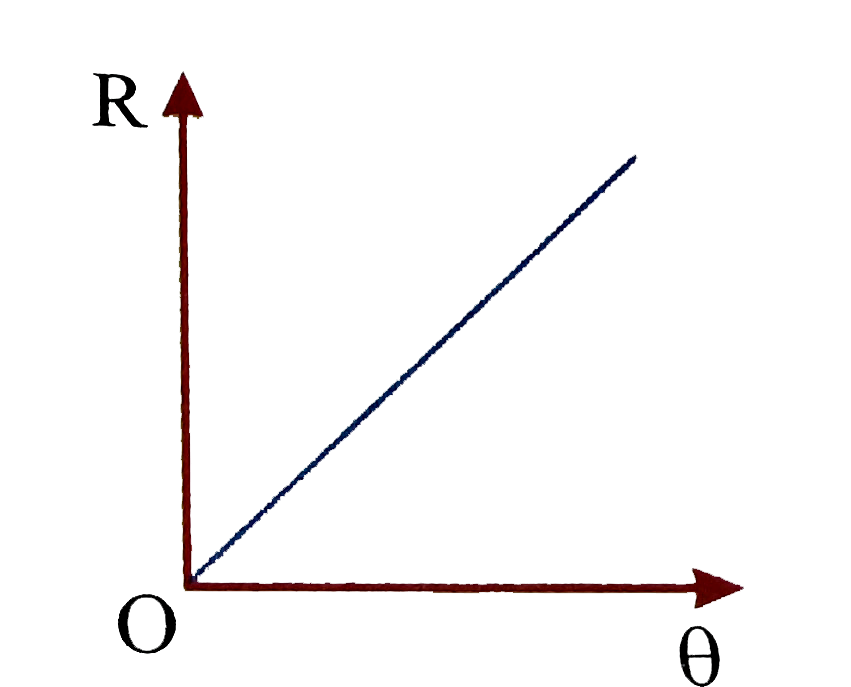 C
C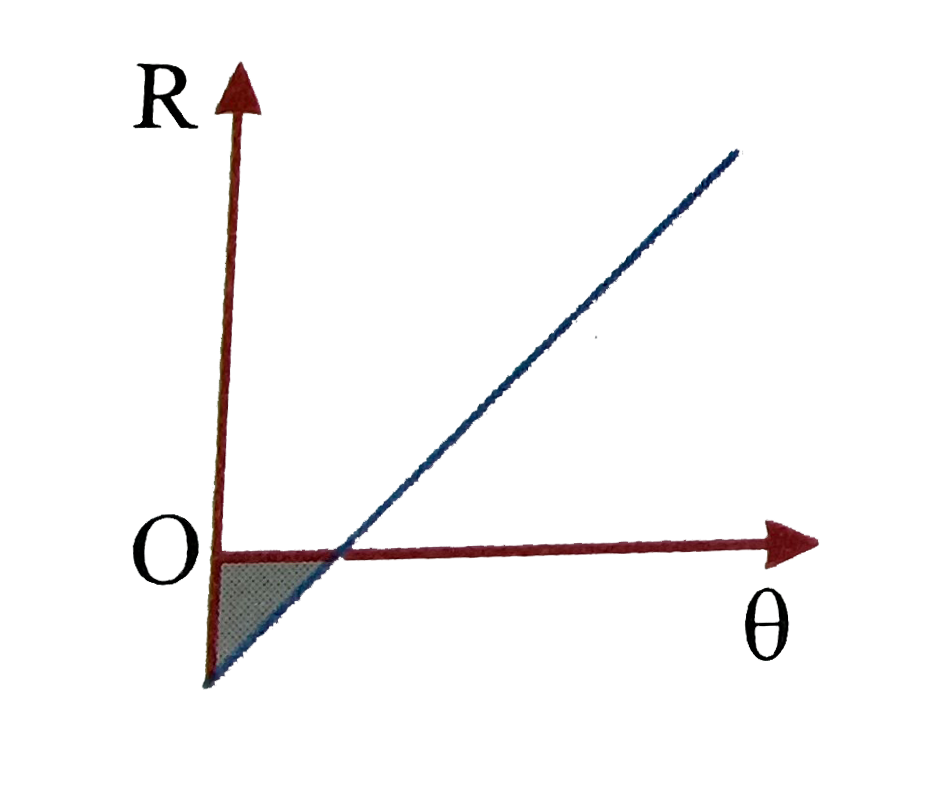 D
D
For a small temperature difference between the body and the surroundings the relation between the rate of loss heat R and the temperature of the body is depicted by
A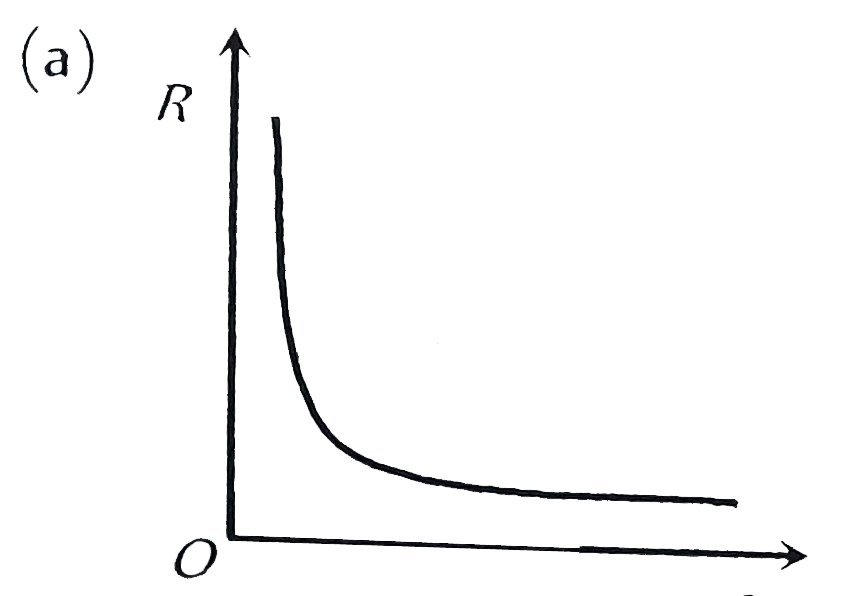 B
B C
C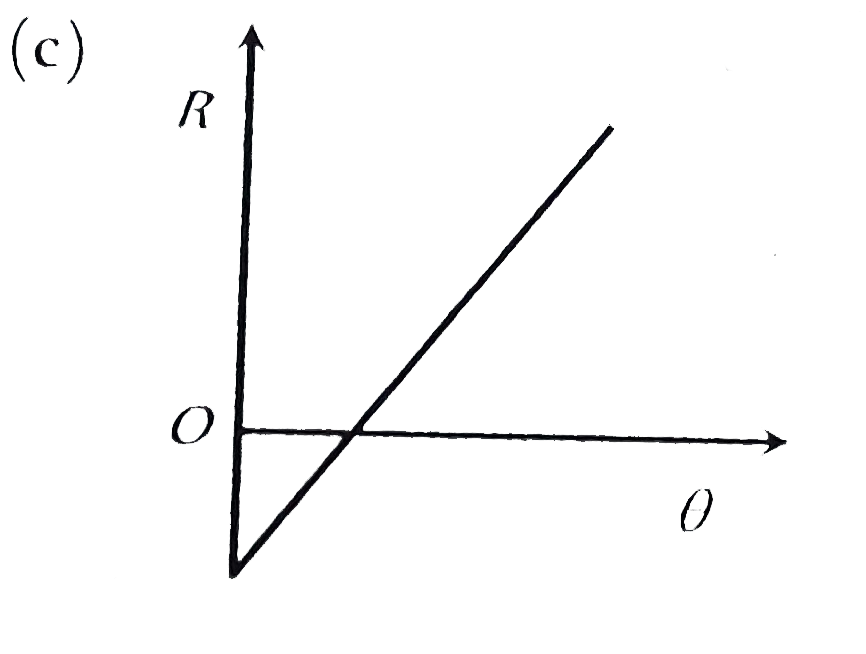 D
D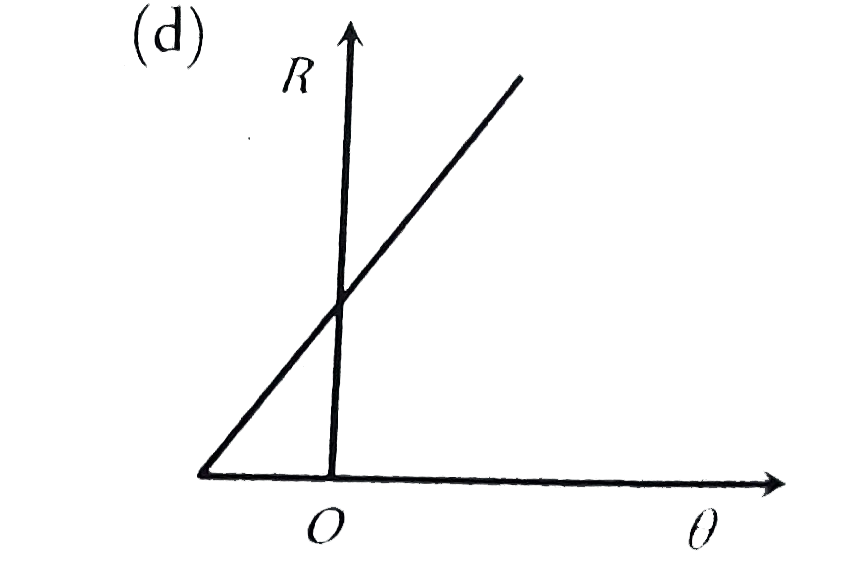
The change in temperature of a body is 20∘C, then the change in temperature of Kelvin scale is :-
A293 KB25 KC20 KD253 K
Change in temperature of a body is 57∘C . The equivalent change in temperature in kelvin scale is ________.
View SolutionBody A has the temperature 100∘F and body B has temperature 100 K. If they are brought in contact, then
View SolutionAs difference of temperature of body and surroundings increases, rate of cooling
View SolutionThe change in temperature of a body is 20∘C, then the change in temperature of Kelvin scale is :-
View SolutionWhen a body has the same temperature as that of its surroundings
View Solution
