A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to produce product A and product B. Each unit of product A required 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs 48 per unit and product B is sold forRs 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income, Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
To solve the problem of maximizing the carpenter's gross income from products A and B using linear programming, we will follow these steps:
Step 1: Define the Variables
Let:
- x = number of units of product A produced
- y = number of units of product B produced
Step 2: Formulate the Objective Function
The objective is to maximize the gross income Z:
Z=48x+40y
Step 3: Formulate the Constraints
Based on the resources available and the requirements for each product, we have the following constraints:
1. Teak Wood Constraint: Each unit of product A requires 2 feet, and each unit of product B requires 1 foot. The total available is 90 feet.
2x+y≤90
2. Plywood Constraint: Each unit of product A requires 1 foot, and each unit of product B requires 2 feet. The total available is 80 feet.
x+2y≤80
3. Rosewood Constraint: Each unit of product A requires 1 foot, and each unit of product B requires 1 foot. The total available is 50 feet.
x+y≤50
4. Non-negativity Constraints: The number of products cannot be negative.
x≥0,y≥0
Step 4: Graph the Constraints
To find the feasible region, we will graph the constraints on a coordinate plane.
1. Graphing 2x+y=90:
- When x=0, y=90 (point (0, 90))
- When y=0, x=45 (point (45, 0))
2. Graphing x+2y=80:
- When x=0, y=40 (point (0, 40))
- When y=0, x=80 (point (80, 0))
3. Graphing x+y=50:
- When x=0, y=50 (point (0, 50))
- When y=0, x=50 (point (50, 0))
Step 5: Identify the Feasible Region
The feasible region is where all the constraints overlap. This region will be bounded by the lines we just graphed and will be in the first quadrant due to the non-negativity constraints.
Step 6: Find the Corner Points of the Feasible Region
To find the corner points of the feasible region, we need to solve the equations of the lines where they intersect:
1. Intersection of 2x+y=90 and x+2y=80:
- Solve the equations:
y=90−2x(from the first equation)
Substitute into the second:
x+2(90−2x)=80⟹x+180−4x=80⟹−3x=−100⟹x=1003≈33.33
Substitute x back to find y:
y=90−2(1003)=90−2003=270−2003=703≈23.33
- Point C(1003,703)
2. Intersection of x+2y=80 and x+y=50:
- Solve:
y=50−x(from the second equation)
Substitute into the first:
x+2(50−x)=80⟹x+100−2x=80⟹−x=−20⟹x=20
Substitute x back to find y:
y=50−20=30
- Point B(20,30)
3. Intersection of 2x+y=90 and x+y=50:
- Solve:
y=50−x
Substitute:
2x+(50−x)=90⟹2x−x+50=90⟹x=40
Substitute x back to find y:
y=50−40=10
- Point A(40,10)
4. Intersection of x+y=50 and the axes gives points (0,50) and (50,0).
Step 7: Evaluate the Objective Function at Each Corner Point
Now we evaluate Z=48x+40y at each corner point:
1. At A(40,10):
Z=48(40)+40(10)=1920+400=2320
2. At B(20,30):
Z=48(20)+40(30)=960+1200=2160
3. At C(1003,703):
Z=48(1003)+40(703)=4800+28003=76003≈2533.33
4. At D(0,50):
Z=48(0)+40(50)=2000
Step 8: Determine the Maximum Value
The maximum value of Z occurs at point A(40,10) with Z=2320.
Conclusion
The carpenter should produce and sell:
- 40 units of product A
- 10 units of product B
Let:
- x = number of units of product A produced
- y = number of units of product B produced
The objective is to maximize the gross income Z:
Z=48x+40y
Based on the resources available and the requirements for each product, we have the following constraints:
2x+y≤90
x+2y≤80
x+y≤50
x≥0,y≥0
To find the feasible region, we will graph the constraints on a coordinate plane.
- When x=0, y=90 (point (0, 90))
- When y=0, x=45 (point (45, 0))
- When x=0, y=40 (point (0, 40))
- When y=0, x=80 (point (80, 0))
- When x=0, y=50 (point (0, 50))
- When y=0, x=50 (point (50, 0))
The feasible region is where all the constraints overlap. This region will be bounded by the lines we just graphed and will be in the first quadrant due to the non-negativity constraints.
To find the corner points of the feasible region, we need to solve the equations of the lines where they intersect:
- Solve the equations:
y=90−2x(from the first equation)
Substitute into the second:
x+2(90−2x)=80⟹x+180−4x=80⟹−3x=−100⟹x=1003≈33.33
Substitute x back to find y:
y=90−2(1003)=90−2003=270−2003=703≈23.33
- Point C(1003,703)
- Solve:
y=50−x(from the second equation)
Substitute into the first:
x+2(50−x)=80⟹x+100−2x=80⟹−x=−20⟹x=20
Substitute x back to find y:
y=50−20=30
- Point B(20,30)
- Solve:
y=50−x
Substitute:
2x+(50−x)=90⟹2x−x+50=90⟹x=40
Substitute x back to find y:
y=50−40=10
- Point A(40,10)
Now we evaluate Z=48x+40y at each corner point:
Z=48(40)+40(10)=1920+400=2320
Z=48(20)+40(30)=960+1200=2160
Z=48(1003)+40(703)=4800+28003=76003≈2533.33
Z=48(0)+40(50)=2000
The maximum value of Z occurs at point A(40,10) with Z=2320.
The carpenter should produce and sell:
- 40 units of product A
- 10 units of product B
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One

Product (A) & (B) respectively are :A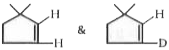 B
B C
C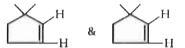 D
D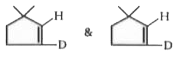

Product C and D are respectively:View Solution
The product B and C are respectively:View SolutionExplain the dot product and cross product of unit vectors.
View Solution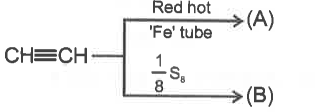 The product (A) & (B) are respectivelyView Solution
The product (A) & (B) are respectivelyView SolutionThe unit to measure productivity is
View Solution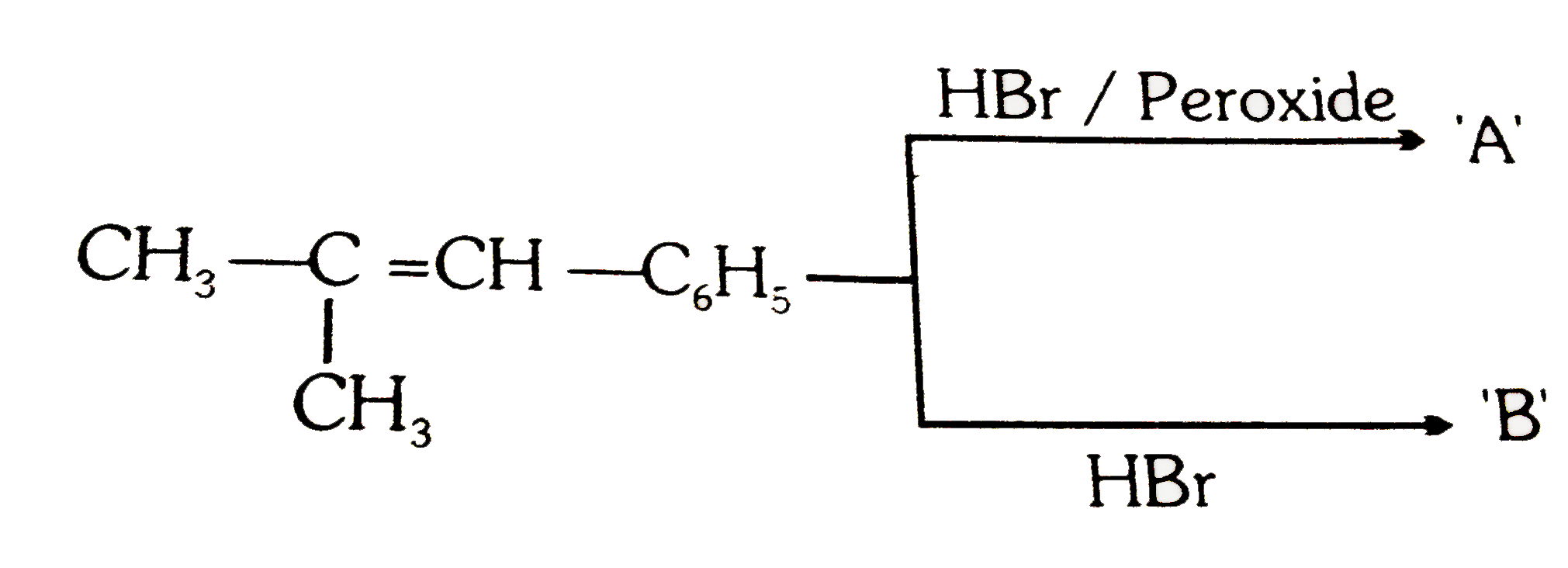
Product 'A' & 'B' are respectively-View SolutionA company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is Rs. 40 on each unit of product of type A and Rs. 50 on each unit of type B. How many units of each type should the company manufacture so as to earn maximum profit ? Use linear programming to find the solution.
View Solution



 , Product B and C are respectively :
, Product B and C are respectively :