A chemicla industry produces two compounds, A and B. The following table gives the units of ingredients C and D (per kg) of compounds A and B as well as minimum requirements of C and D, and costs per kg of A and B.

Find the quantities of A and B which would minimize the cost.
Let x kg of A and y kg of B be produced. Then
x≥0,y≥0,x+2y≥80and3x+y≥75.
Then cost function is given by Z=4x+6y.
Thus, we have to minimize Z=4x+6y, suvject to the constraints:
x≥0,y≥0,x+2y≥80and3x+y≥75.
Draw the graphs of the lines
x=0,y=0,x+2y=80and3x+y=75.

Since (0,0) does not satisfy the inequation x+2y≥80, the line x+2y=80 together with the regin not containing (0,0) represents x+2y≥75.
Since (0,0) does not satisfy the inequation 3x+y≥75, the line 3x+y=75 together with the rigion not containing (0,0) represents 3x+y≥75.
Thus, the shaded regio is the feasible region.
The vertices of this region are P, Q and R.
On solving x=0and3x+y=75, we get the point Q(14,33). On solving y=0andx+2y=80, we get the point R(80,0).
The valuse of Z=4x+6y at the point P(0,75),Q(14,33)andR(80,0) are 450,254and320 respectively.
Thus, Z is minimum at Q(14,33).
Hence, for a minimum, cost, 14 kg of A and 33 kg of B must be taken.
Similar Questions
A compound 'A' when reacts with LiAlH4 it gives two compounds B and C along with LiCl. Compounds A, B and C respectively are
View SolutionA company owns two coal mines, A and B say. The production in these mines and the total requirement are given in the table below :
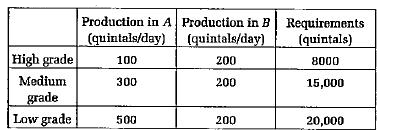
How many days should each mine be operated if it costs Rs. 500 per day to work each mine so that the total cost incurred is minimized when the requirements are satisfied ?
View Solution
Knowledge Check
Food X contains 4 units of vitamin A per gram and 7 units of vitamin B per gram and cost 15 paise per gram . Food Y contains 6 units of vitamin A per gram and 11 units of vitamin B per gram and cost 22 paise per gram . The daily minimum requirement of vitamin A and B are 90 units and 130 units respectively . The formulation of LPP to minimize the cost is
Az = 15x +22y, subject to constraints 4x+6y≥90,7x+11y≥130,x≥0y≥0Bz = 6x +5y, subject to constraints 4x+3y≥90,7x+11y≥130,x≥0y≥0Cz = 15x +62y, subject to constraints 4x+6y≥90,7x+11y≥450,x≥0y≥0Dz = 15x +22y, subject to constraints 4x+6y≥90,7x+45y≥260,x≥0y≥0Two different kinds of food A and B are being considered to form a weekly diet . The minimum weekly requirements for fats , carbohydrates and protein are 18, 24 and 16 units respectively . One kg of food A has 4 , 16 , and 8 units respectively of these ingredients and one kg of food B has 12 ,4 and 6 units respectively The price of food A is Rs 6 per kg and that of food B is Rs 5 per kg. How many kg of each type of food should he buy per week to minimize the cost and meet his requirements . Formulate this LPP
Az = 15 x+22y, subject to contraints 4x+12y≥18,16x+4y≥24,8x+6y>16,x≥0y≥0Bz = 15x +22y, subject to constraints 4x+12y≥18,16x+4y≥24,8x+6y>16,x≥0y≥0Cz=15x+48y , subject to constraints 4x+12y≥18,17x+4y≥24,8x+6y>160,x≥0y≥0Dz = 15x +22y, subject to constraints 24x+12y≥18,18x+4y≥24,8x+16y>16,x≥0y≥0A dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C . Food I contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C , while food II contains 1 unit per kg of vitamin A and 2 units per kg of vitamin C . It costs Rs 5 per kg to purchase food I and Rs 7 per kg to purchase food II . Identify the objective function so as to minimize the cost of mixture.
AMaximize z=5x+7yBMinimize z=2x+yCMaximize z=2x+2yDMinimize z=7x+2y
Food X contains 6 units of vitamin A per gm and 7 units of vitamin B per gm and costs ₹ 2.00 per gm.Food Y contains 8 units of Vitamin A per gm and 12 units of vitamin B per gm and costs ₹ 2.50 per gm.The daily minimum requirement of vitamin A and vitamin V are 100 units and 120 units respectively.Formulate the above as a linear programming problem to minimize the cost.
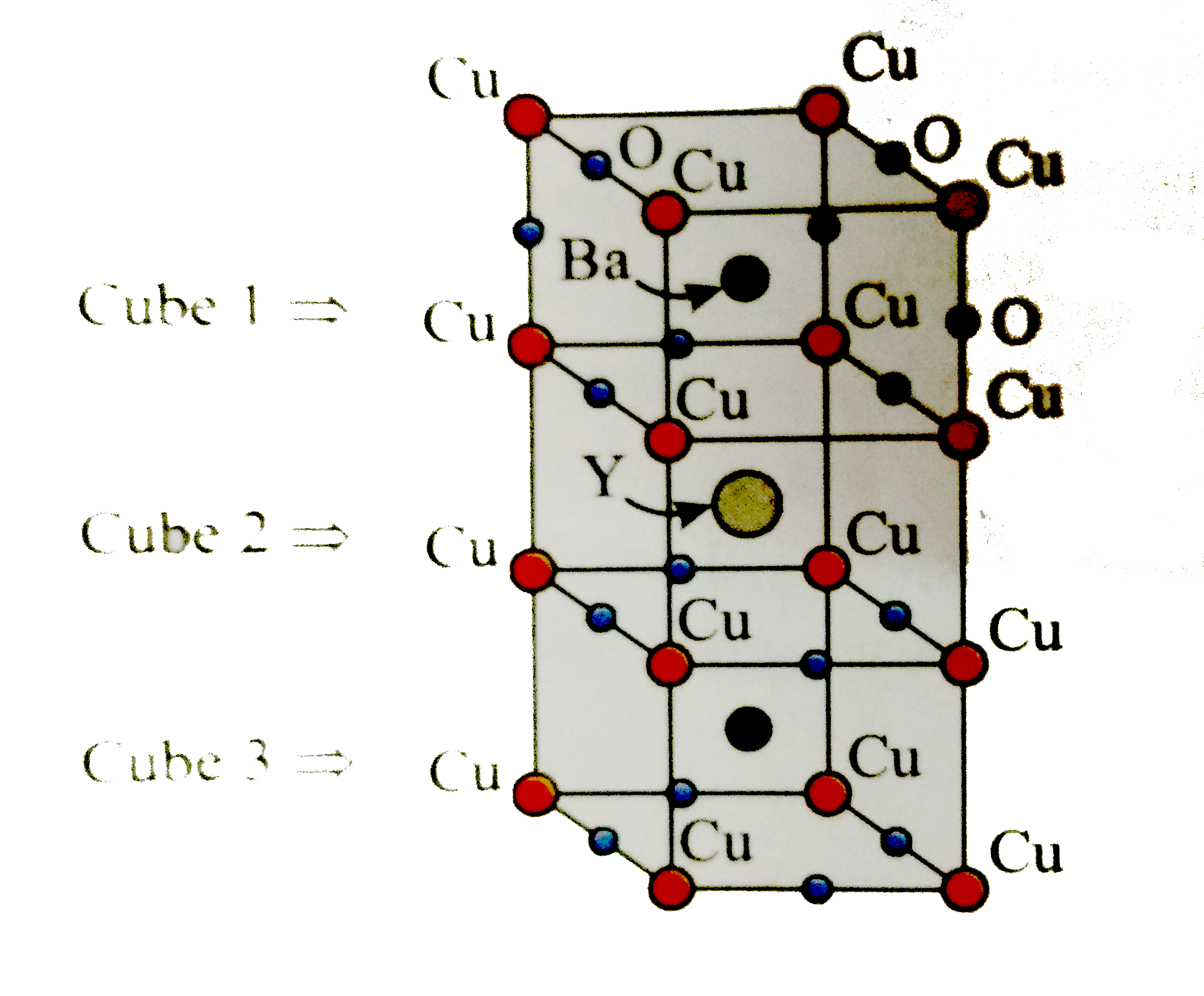
View SolutionThe following figure shows the unit cell of a compound, i.e., a mixed oxide of yttrium, barium , and copper. The formula of mixed oxide is YaBabCucOd . Find the value of (c+d)−(a−b).
View SolutionThe following pie chart shows the percentage quantity of fruits at two fruit shops A and B.
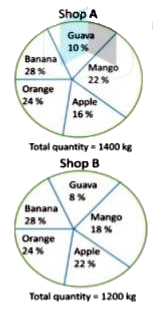
If the price of apple is Rs50 per kg and that of orange of is Rs 25 kg. then what is the ratio their costs at shop A ?
View SolutionThe following figure shows the unit cell of a compound, i.e., a mixed oxide of yttrium, bariym, and copper. The formula of mixed oxide is YaBabCucOd.
Find the value of (a+b+c+d).

View SolutionA dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of Vitamin A and 10 units of vitamin C, Food I contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C while food II contains 1 unit per kg of vitamin A and 2 units per kg of vitamin C. It costs Rs 50.00 per kg to purchase food I and Rs. 70.00 per kg to produce food II. Formulate the above linear programming problem to minimize the minimize the cost of such a mixture.
View Solution
