A chord of a circle subtends an angle of 60∘ at the centre. If the length of the chord is 100 cm, then find the area of the major segment.
30720.5cm2
31021cm2
30391.7cm2
26190.47cm2
The correct Answer is:D
To find the area of the major segment of a circle given that a chord subtends an angle of 60∘ at the center and the length of the chord is 100 cm, we can follow these steps:
Step 1: Understand the Geometry
We have a circle with center O and a chord AB that subtends an angle of 60∘ at the center. The points A and B are on the circumference of the circle.
Step 2: Find the Radius
Since the chord AB subtends an angle of 60∘ at the center, we can use the properties of triangles to find the radius r.
In triangle OAB, we know:
- OA=OB=r (radii of the circle)
- AB=100 cm (length of the chord)
Using the formula for the length of a chord:
AB=2rsin(θ2)
where θ is the angle subtended at the center.
Substituting the known values:
100=2rsin(30∘)
Since sin(30∘)=12:
100=2r⋅12
100=r
Thus, the radius r is 100 cm.
Step 3: Calculate the Area of the Sector
The area A of the sector formed by the angle 60∘ is given by the formula:
A=θ360⋅πr2
Substituting θ=60∘ and r=100 cm:
A=60360⋅π⋅(100)2
A=16⋅π⋅10000
A=10000π6≈5235.99 cm2
Step 4: Calculate the Area of the Triangle
The area AT of triangle OAB can be calculated using the formula:
AT=12⋅OA⋅OB⋅sin(θ)
Substituting the known values:
AT=12⋅100⋅100⋅sin(60∘)
Since sin(60∘)=√32:
AT=12⋅100⋅100⋅√32
AT=2500√3≈4330.13 cm2
Step 5: Calculate the Area of the Major Segment
The area of the major segment is the area of the sector minus the area of the triangle:
Amajor segment=A−AT
Amajor segment=10000π6−2500√3
Substituting the approximate values of π≈3.14 and √3≈1.732:
Amajor segment≈10000⋅3.146−2500⋅1.732
Amajor segment≈5235.99−4330.13≈905.86 cm2
Final Answer
The area of the major segment is approximately 905.86 cm2.
We have a circle with center O and a chord AB that subtends an angle of 60∘ at the center. The points A and B are on the circumference of the circle.
Since the chord AB subtends an angle of 60∘ at the center, we can use the properties of triangles to find the radius r.
- OA=OB=r (radii of the circle)
- AB=100 cm (length of the chord)
AB=2rsin(θ2)
where θ is the angle subtended at the center.
100=2rsin(30∘)
Since sin(30∘)=12:
100=2r⋅12
100=r
Thus, the radius r is 100 cm.
The area A of the sector formed by the angle 60∘ is given by the formula:
A=θ360⋅πr2
Substituting θ=60∘ and r=100 cm:
A=60360⋅π⋅(100)2
A=16⋅π⋅10000
A=10000π6≈5235.99 cm2
The area AT of triangle OAB can be calculated using the formula:
AT=12⋅OA⋅OB⋅sin(θ)
Substituting the known values:
AT=12⋅100⋅100⋅sin(60∘)
Since sin(60∘)=√32:
AT=12⋅100⋅100⋅√32
AT=2500√3≈4330.13 cm2
The area of the major segment is the area of the sector minus the area of the triangle:
Amajor segment=A−AT
Amajor segment=10000π6−2500√3
Substituting the approximate values of π≈3.14 and √3≈1.732:
Amajor segment≈10000⋅3.146−2500⋅1.732
Amajor segment≈5235.99−4330.13≈905.86 cm2
The area of the major segment is approximately 905.86 cm2.
Topper's Solved these Questions
- SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020EXERCISE - EVERYDAY MATHEMATICS
10 Videos
- SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020EXERCISE - ACHIEVERS SECTION
4 Videos
- SAMPLE PAPER 4 (CLASS 10)BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SAMPLE PAPER 4 (CLASS 10)EXERCISE - Section E - Logical Reasoning
1 Video
- SOME APPLICATIONS OF TRIGONOMETRY BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOME APPLICATIONS OF TRIGONOMETRY EXERCISE - ACHIEVERS SECTION (HOTS)
5 Videos
Similar Questions
Knowledge Check
The chord of a circle of radius 10cm subtends a right angle at its centre. The length of the chord (in cm) is
A5√2B5√2C10√2D10√3A chord of length 7 cm subtends an angle of 60∘ at the centre of a circle. What is the radius (in cm) of the circle?
A7√2B7√3C7D14A chord of length 7 cm subtends an angle of 60∘ at the centre of a circle. What is the radius (in cm) of the circle?
A7√2B7√3C7D14
A chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the minor and major segments. [Take π=314 and √3=1.732]
View SolutionA chord PQ of a circle of radius 10 cm makes an angle of 60∘ at the centre of the circle. Find the area of the major and the minor segment
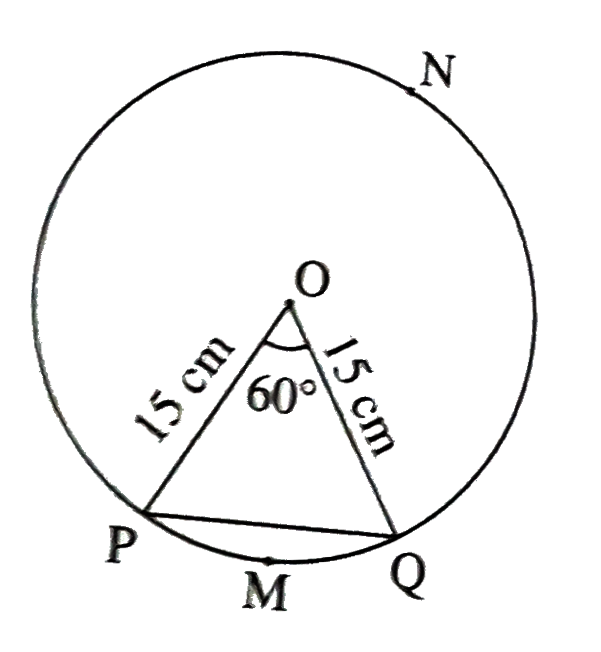
View SolutionA chord PQ of a circle with radius 15 cm subtends an angle of 60∘ with the centre of the circle. Find the area of the minor as well as the major segment. (π=3.14,√3=1.73)
View SolutionThe chord of a circle of radius 8 cm subtends a right angle at its centre. Find the length of the chord.
View SolutionA chord of length 10 cm subtends an angle 120∘ at the centre of a circle . Distance of the chord from the centre is
View Solution