A circle is drawn in a sectore of a larger circle of radius r, as shown in fugure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the smaller circle is
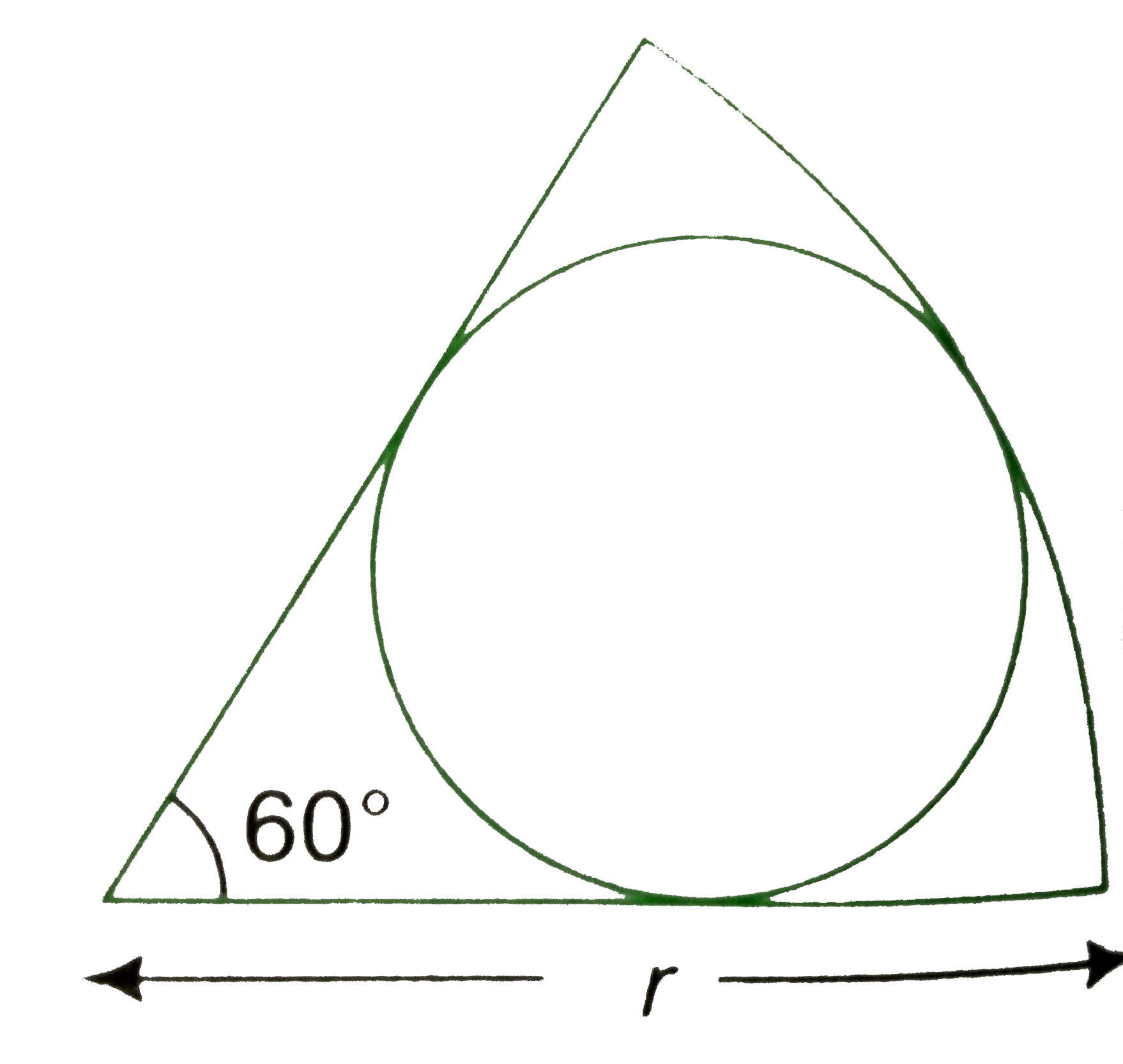
r2
r3
2√3r5
r√2
The correct Answer is:A
Let the radius of smaller circle be x. Here,
OP=xcosec30∘
andOQ=r=xcosec30∘
⇒=x=r3

Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Correct Answers Type
17 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Linked Comprehension Type
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.14
1 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
A circle is drawn in a sector of a larger circle of radius r, as shown in the adjacent figure. The smaller circle is tangent to the two bounding radii and the are of the sector. The radius of the small circle is-

View Solution(c) 103 (d) 10 18. A circle is inscribed in an equilateral triangle with side lengths 6 unit. Another circle is drawn inside the triangle (but outside the first circle), tangent to the first circle and two of the sides of the triangle. The radius of the smaller circle is (b) 2/3 (a) 1/ root3 (c) 2 (d) 1
View SolutionThe adjoining figure shows two circles with the same centre. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between two circles ( π=3.14)
View SolutionAn arc of a circle is a length 5πcm and the sector it bounds has an area of 20πcm2 . Find the radius of the circle.
View SolutionWrite the area of the sector of a circle whose radius is r and length of the arc is l .
View SolutionFind the area of a sector of a circle of radius 28cm and central angle 45∘.
View SolutionTwo concentric circles are such that the smaller divides the larger into two regions of equal area. If the radius of the smaller circle is 2, then the length of the tangent from any point 'P'on the larger circle to the smaller circle is
View SolutionFind the area of a sector of a circle with radius 6 cm if angle of the sector is 60∘
View SolutionThe area of a sector of a circle of radius 5 cm is 5 π cm2 . Find the angle contained by the sector
View SolutionA sector of a circle of radius 8 cm contains an angle of 135o . Find the area of the sector.
View Solution
