A circle is inscribed in a triangle ABC touching the side AB at D such that AD=5,BD=3,if∠A=600 then length BC equals. 9 (b)12013(c) 13(d) 12
9
12013
13
12
The correct Answer is:C

tan30∘=r5
or r=5√3
We have tan.B2=r3=53√3...(i)
∴cosB1−tan2.B21+tan2.B2=126
∴sinB=√67526=15√326
∴sinC=sin(A+B)=sinAcosB+cosAsinB=4√313
Now asinA=csinC⇒a=13
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise (Multiple)
Explore 24 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise (Comprehension)
Explore 34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.11
Explore 4 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
A circle is inscribed in a triangle ABC touching the side AB at D such that AD=5,BD=3,if∠A=600 then length BC equals. 9 (b)12013(c) 13(d) 12
View SolutionA circle is inscribed in a ABC having side 8cm,10cmand12cm as shown in Figure. Find AD,BEandCF.
View SolutionSide BC of a triangle ABC has been produced to a point D such that ∠1200. If ∠B=12∠A, then ∠A is equal to 800 (b) 750 (c) 600 (d) 900
View Solution9+|−4| is equal to: 5 (b) −5 (c) 13 (d) −13
View SolutionLet aandb represent the lengths of a right triangles legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle circumscribed on the triangle, the d+D equals. (a)a+b (b) 2(a+b) (c)12(a+b) (d) √a2+b2
View SolutionFigure shows triangle ABC such that AB=AC=5,BC=6.P∮DisonB Csuchtˆ(B D)/(D C)=1/2,then□of≤n>hofsA D is
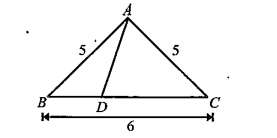
View SolutionIf a,b, A are given in a triangle and c1and c2 are two possible values of third side such that c21+c1c2+c22=a2 , then A is equal to 300 (b) 600 (c) 900 (d) 1200
View SolutionIn a rhombus ABCD, if ∠ACB=40∘, then ∠ADB=(a) 70∘ (b) 45∘ (c) 50∘ (d) 60∘
View SolutionIn A B C, if AB=10,BC=8,CA=12 and a point D is taken on AB such that A D: D B is 3:2 , then the square of length of CD is
View SolutionIn a triangle ABC , if B=300and c=√3 b, then A can be equal to 450 (b) 600 (c) 900 (d) 120^0
View Solution