A circular ring of radius 3 cm is suspended horizontally from a point 4 cm vertically above the centre by 4 strings attached at equal intervals to its cirumference . If the angle between two consecutive strings be θ, then cos(θ)-
45
425
1625
none of these
The correct Answer is:C
Let O be the centre of the circular ring which is suspended by the strings PA, PB, PC and PD in such a way that P is just above the point O and arcAB=arcBC=arcCD=arcAD.

∴∠AOB=90∘
Also, in △AOP, we have
AP=√OA2+OP2=√32+42=5
⇒ BP=AP=5
In △APB , we have
cosθ=AP2+BP2−AB22AP.BP
⇒cosθ=52+52−(3√2)22×5×5[In△AOB,AB2=OA2+OB2]
⇒cosθ=1625
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - OBJECTIVE RD SHARMACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise
45 Videos
- EXPONENTIAL AND LOGARITHMIC SERIESBOOK - OBJECTIVE RD SHARMACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIESEXERCISE - Chapter Test
20 Videos
- INCREASING AND DECREASING FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - INCREASING AND DECREASING FUNCTIONSEXERCISE - Chapter Test
20 Videos
Similar Questions
A circular ring of radius 3cm hangs horizontally form a point 4cm vertically above the centre by 4 strings attached at equal intervals to its circumference. If the angle between two consecutive strings be θ , then cosθ is equal to (A)45 (B) 425 (C) 1625 (D) none of these
View SolutionA ring,10 cm in diameter, is suspended from a point 12cm above its centre by 6 equal strings attached to its circumference at equal intervals. Find the cosine of the angle between consecutive strings.
View Solution
Knowledge Check
A circular ring of radius 5 cm is suspended horizontally from a point 12 cm vertically above its centre by 6 strings attached to its circumference at equal intervals. The cosine of the angle between two consecutive ring is
A12B1213C313338Dnone of these of theseA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
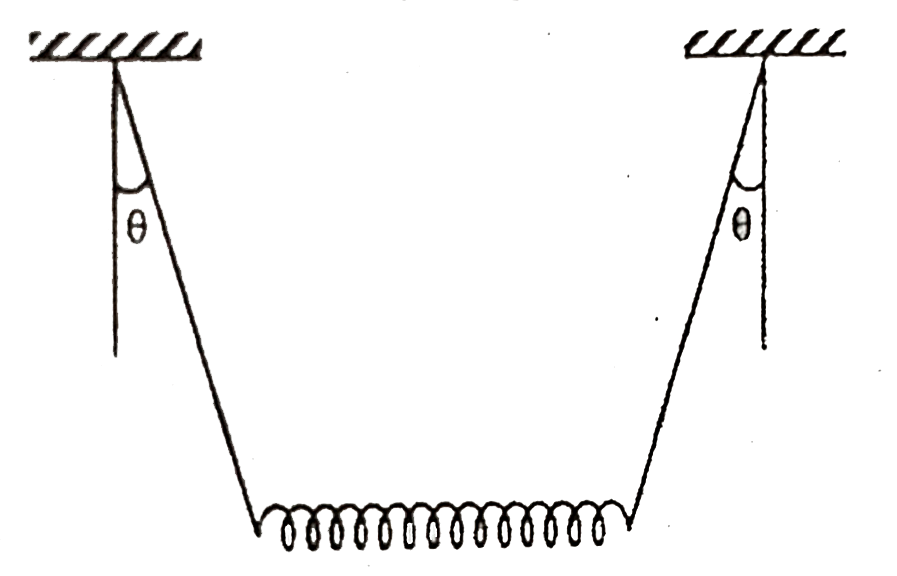 A(W/4k)tanθB(W/2k)tanθC(W/4k)sinθD0
A(W/4k)tanθB(W/2k)tanθC(W/4k)sinθD0A uniform one metre long rod AB of weight 17 kg is suspended horizontally from fixed supports by two vertical strings attached to points C and D on the rod at distances of 12 cm and 16 cm from A and B respectively. The strings at C and D can support weights of 10 kg and 9 kg respectively without breaking. Then the position where a weight of 2 kg can be attached to the rod without breaking either of the strings is
A10 cm from AB12 cm from AC13 cm from ADNone of these
A uniform one metre long rod AB of 17 kg weight I suspended horizontally from fixed supports by two vertical strings attached to points C and D on the rod at distances of 12 cm and 16 cm from A and B respectively .The strings at C and D can support weights of 10 kg and 9 kg respectively without breaking .Find where a weight of 2 kg can be attached to the rod without breaking either of the string .
View SolutionA circular ring of weight 4kg and radius 60 cm is suspended on a horizontal nail at its circumference. The frequency of oscillation for small oscillations was found to be____Hz. (Take √8.17=2.85)
View SolutionLength of a tangent drawn to a circle with radius 3 cm from a point 4 cm from the centre of the circle is
View Solution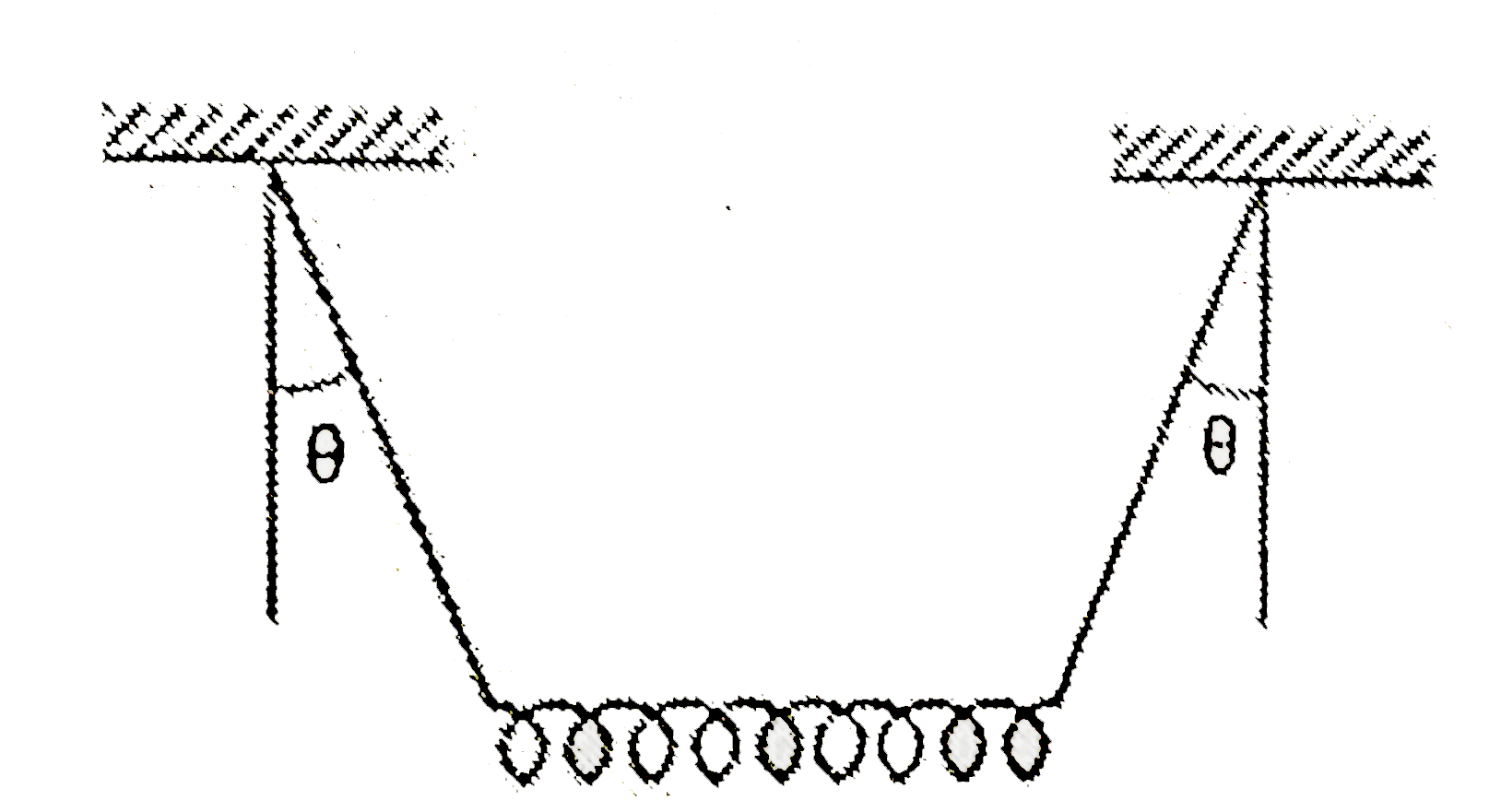
Aspring of weight W and force constant k is suspended in a horizontal position by two light strings attached to its two ends. Each string makes and angle θ with the vertical .The extension of the sporing is
View SolutionA uniform rod of length 15 cm is suspended from a fixed point by two strings of length 9 cm and 12 cm attached at its ends. If the inclination of the rod to the vertical is θ then sinθ is equal to
View Solution
