A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.
To find the mean number of days a student was absent based on the absentee record of 40 students, we will follow these steps:
Step 1: Organize the Data
First, we need to organize the absentee data into a frequency distribution table. We will create intervals for the number of days absent and count how many students fall into each interval.
| Days Absent (Interval) | Frequency (f) |
|------------------------|---------------|
| 0 - 6 | 11 |
| 6 - 10 | 10 |
| 10 - 14 | 7 |
| 14 - 20 | 4 |
| 20 - 28 | 4 |
| 28 - 38 | 3 |
| 38 - 40 | 1 |
Step 2: Calculate the Midpoint (x)
Next, we calculate the midpoint (x) for each interval. The midpoint is found by taking the average of the lower and upper limits of each interval.
| Days Absent (Interval) | Frequency (f) | Midpoint (x) |
|------------------------|---------------|---------------|
| 0 - 6 | 11 | 3 |
| 6 - 10 | 10 | 8 |
| 10 - 14 | 7 | 12 |
| 14 - 20 | 4 | 17 |
| 20 - 28 | 4 | 24 |
| 28 - 38 | 3 | 33 |
| 38 - 40 | 1 | 39 |
Step 3: Calculate f * x
Now, we will multiply the frequency (f) by the midpoint (x) for each interval to get the values of f * x.
| Days Absent (Interval) | Frequency (f) | Midpoint (x) | f * x |
|------------------------|---------------|---------------|-------|
| 0 - 6 | 11 | 3 | 33 |
| 6 - 10 | 10 | 8 | 80 |
| 10 - 14 | 7 | 12 | 84 |
| 14 - 20 | 4 | 17 | 68 |
| 20 - 28 | 4 | 24 | 96 |
| 28 - 38 | 3 | 33 | 99 |
| 38 - 40 | 1 | 39 | 39 |
Step 4: Sum of Frequencies (Σf) and Sum of f * x (Σf * x)
Now, we need to calculate the total of frequencies and the total of f * x.
- Σf = 11 + 10 + 7 + 4 + 4 + 3 + 1 = 40
- Σ(f * x) = 33 + 80 + 84 + 68 + 96 + 99 + 39 = 499
Step 5: Calculate the Mean
Finally, we can calculate the mean number of days absent using the formula:
Mean=Σ(f⋅x)Σf=49940=12.475
Conclusion
The mean number of days a student was absent is 12.475.
---
First, we need to organize the absentee data into a frequency distribution table. We will create intervals for the number of days absent and count how many students fall into each interval.
|------------------------|---------------|
| 0 - 6 | 11 |
| 6 - 10 | 10 |
| 10 - 14 | 7 |
| 14 - 20 | 4 |
| 20 - 28 | 4 |
| 28 - 38 | 3 |
| 38 - 40 | 1 |
Next, we calculate the midpoint (x) for each interval. The midpoint is found by taking the average of the lower and upper limits of each interval.
|------------------------|---------------|---------------|
| 0 - 6 | 11 | 3 |
| 6 - 10 | 10 | 8 |
| 10 - 14 | 7 | 12 |
| 14 - 20 | 4 | 17 |
| 20 - 28 | 4 | 24 |
| 28 - 38 | 3 | 33 |
| 38 - 40 | 1 | 39 |
Now, we will multiply the frequency (f) by the midpoint (x) for each interval to get the values of f * x.
|------------------------|---------------|---------------|-------|
| 0 - 6 | 11 | 3 | 33 |
| 6 - 10 | 10 | 8 | 80 |
| 10 - 14 | 7 | 12 | 84 |
| 14 - 20 | 4 | 17 | 68 |
| 20 - 28 | 4 | 24 | 96 |
| 28 - 38 | 3 | 33 | 99 |
| 38 - 40 | 1 | 39 | 39 |
Now, we need to calculate the total of frequencies and the total of f * x.
- Σ(f * x) = 33 + 80 + 84 + 68 + 96 + 99 + 39 = 499
Finally, we can calculate the mean number of days absent using the formula:
The mean number of days a student was absent is 12.475.
Similar Questions
Knowledge Check
The students in three classes are in the ratio of 2:3:4. If 40 students are added in each clas, the ratio becomes 4:5:6. Find the total number of students in all the three classes is :
A270B180C126D135There are 40% girls in a class of 50 students. Find the number of boys in the class
A20B10C25D30To maintain interest among students in class, a teacher should:
AUse balckboardBDiscussCTell storiesDAsk question
If 30 of the 36 students of a class were present on a certain day,what percentage of students were absent?
View SolutionAnswer the following questions
Find the ratio of students of class sixth to the students of class eight

View SolutionIn Class XI of a certain school, there are 30 students in a Mathematics class and 20 students in Biolog class. Find the number of students which are in Mathematics class or in Biology class in the following cases:
(i) Two classes are conducted at the same time.
(ii) Two classes are condcuted at different time and 5 students study both the subject
View SolutionFollowing is the data showing weights of 40 students in a class . Find its median .
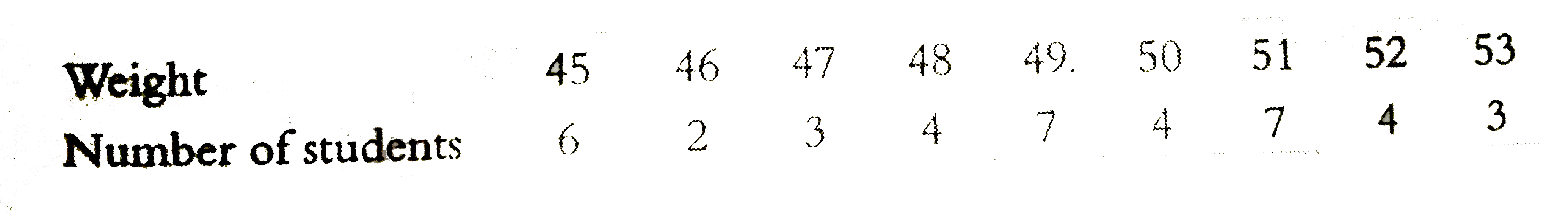
View SolutionA school keeps medical record of all the students. Following table shows the gain in weights by 40 students of Class X in a year. Find the median gain in weight.
View Solution

