A coin is tossed until a head appears or the tail appears 4 times in succession. Find the probability distribution of the number of tosses.
To solve the problem of finding the probability distribution of the number of tosses when a coin is tossed until a head appears or a tail appears four times in succession, we will follow these steps:
Step 1: Define the Random Variable
Let X be the random variable representing the number of tosses until we either get a head (H) or four tails (T) in succession.
Step 2: Identify Possible Outcomes
We will identify the possible outcomes based on the conditions given:
- If the first toss is a head (H), then X=1.
- If the first toss is a tail (T), we can have the following sequences:
- T, H (2 tosses)
- T, T, H (3 tosses)
- T, T, T, H (4 tosses)
- T, T, T, T (4 tosses)
Step 3: Calculate Probabilities for Each Outcome
1. Probability of X=1:
- The only outcome is H.
- P(X=1)=P(H)=12.
2. Probability of X=2:
- The outcome is T, H.
- P(X=2)=P(T)⋅P(H)=12⋅12=14.
3. Probability of X=3:
- The outcome is T, T, H.
- P(X=3)=P(T)⋅P(T)⋅P(H)=12⋅12⋅12=18.
4. Probability of X=4:
- The outcomes can be either T, T, T, H or T, T, T, T.
- P(X=4)=P(T)⋅P(T)⋅P(T)⋅P(H)+P(T)⋅P(T)⋅P(T)⋅P(T)
- P(X=4)=(12⋅12⋅12⋅12)+(12⋅12⋅12⋅12)=116+116=18.
Step 4: Summarize the Probability Distribution
Now we can summarize the probability distribution of the random variable X:
XP(X)112214318418
Conclusion
The probability distribution of the number of tosses until a head appears or four tails appear in succession is given by the table above.
---
Let X be the random variable representing the number of tosses until we either get a head (H) or four tails (T) in succession.
We will identify the possible outcomes based on the conditions given:
- If the first toss is a head (H), then X=1.
- If the first toss is a tail (T), we can have the following sequences:
- T, H (2 tosses)
- T, T, H (3 tosses)
- T, T, T, H (4 tosses)
- T, T, T, T (4 tosses)
1. Probability of X=1:
- The only outcome is H.
- P(X=1)=P(H)=12.
- The outcome is T, H.
- P(X=2)=P(T)⋅P(H)=12⋅12=14.
- The outcome is T, T, H.
- P(X=3)=P(T)⋅P(T)⋅P(H)=12⋅12⋅12=18.
- The outcomes can be either T, T, T, H or T, T, T, T.
- P(X=4)=P(T)⋅P(T)⋅P(T)⋅P(H)+P(T)⋅P(T)⋅P(T)⋅P(T)
- P(X=4)=(12⋅12⋅12⋅12)+(12⋅12⋅12⋅12)=116+116=18.
Now we can summarize the probability distribution of the random variable X:
The probability distribution of the number of tosses until a head appears or four tails appear in succession is given by the table above.
Similar Questions
A coin is tossed until a head appears or the tail appears 4 times in succession. Find the probability distribution of the number of tosses.
View SolutionA fair die is tossed twice. If the number appearing on the top is less than 3, it is a success. Find the probability distribution of number of successes.
View Solution
Knowledge Check
- Question 1 - Select One
Three coins are tossed. Then the probability distribution of number of head is
A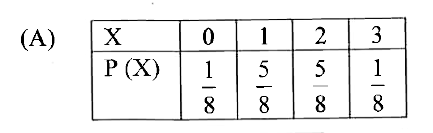 B
B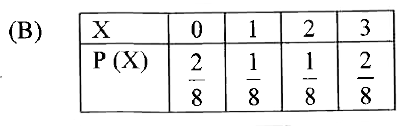 C
C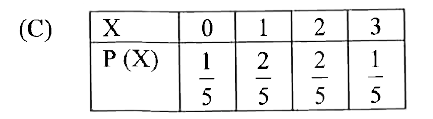 D
D
- Question 2 - Select One
A biased coin with probability p,0<p<1 of heads is tossed until a head appears for the first time . If the probability that the number of tosses required is even is 2/5, then p equals
A14B13C34D12 - Question 3 - Select One
A biased coin with probability p(0<p<1) of getting heads, is tossed until a head appears for the first time. If the probability that the number of tosses required is even is 1/5, then p is equal to…….
A34B16C13D14
A coin is tossed 4 times. Find the mean and variance of the probability distribution of the number of tails.
View SolutionA biased coin with probability p, 0<p<1 of heads is tossed until a head appears for the first time. If the probability that the number of tosses required is even is 2/5, then p equals
View Solution(a) (i) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
(ii) Find the probability distribution of the number of tails in the simultaneous tosses of three coins.
(iii) Find the probability distribution of the number of heads in the simultaneous toss of four coins.
(b) (i) Find the probability distribution of the number of heads in three tosses of a coin.
(ii) Find the probability distribution of the number of sixes in two tosses of a die.
( c ) Find the probability distribution of the number of heads (tails) in four tosses of a coin.View SolutionA biased coin is tossed repeatedly until a tail appears for the first time. The head is 3 times likely to appear as the tail. The probability that the number of tosses required will be more than 4, given that in first two toss no tail has occur, is
View SolutionA biased coin with probability p(0<p<1) of falling tails is tossed until a tail appears for the first time. If the probability that tail comes in odd number of trials is 23, then p equals
View Solution
