Question

A company makes two kinds of leather belts, A and B. Belt A is high
quality belt, and B is of lower quality. The respective profits are Rs. 40
and Rs. 30 per belt. Each belt of type A requires twice as much time as a
belt of type B, and if all belts were of type B, the company could make 1000
belts per day. The supply of leather is sufficient for only 800 belts per day
(both A and B combined). Belt A requires a fancy buckle, and only 400 buckles
per day are available. There are only 700 buckles available for belt B. What
should be the daily production of each type f belt? Formulate the problem as
a LPP.

Explanation

Let x belts of type A and y belts of type B be made. Then `x ge 0m,yge 0,x le400, y le 700 and x+yle800.`
Now, 1000 belts of type B can be made in 1 day.
`therefore` 500 belts of type A can be made in 1 day.
`therefore` time taken to make x belts of type A and y belts of type B `=((x)/(500)+(y)/(1000))days.`
`therefore(x)/(500)+(y)/(1000)le1,i.e., 2x+y le1000.`
We have to maximize `Z=4x+3y,` subject to the constraints `x ge0,yge0,xle400, yle700,x+yle800and 2x+y le1000.`
We draw the graphs of the lines
`x=0,y=0,x=400,y=700,x+y=800,2x+y=1000` as shown below.

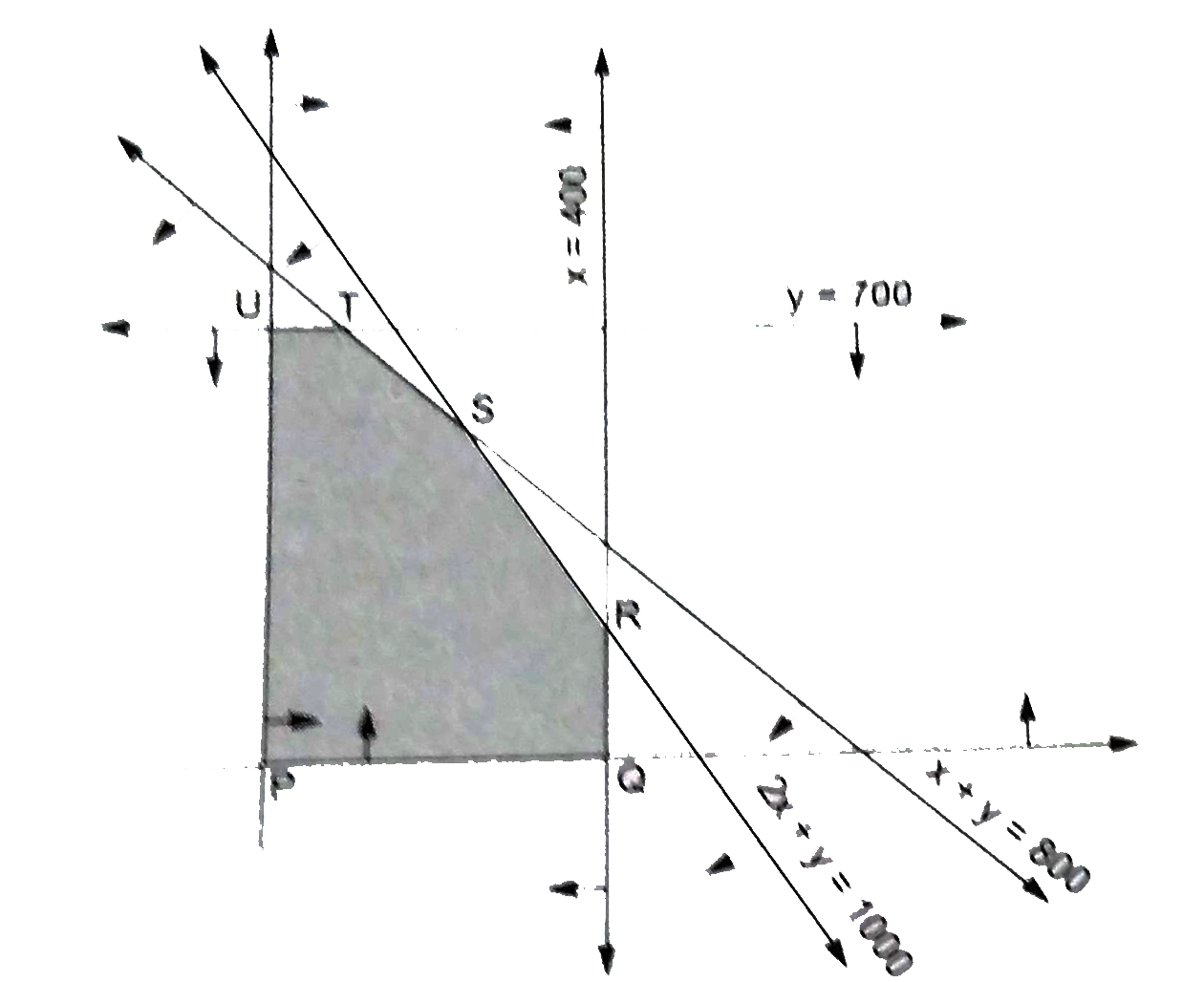
Since (0,0) satisfies `x le400,` line x=400 together with the region containing `O(0,0)` represents `x le400.`
Since (0,0) satisfies `y le700,`
Since `(0,0)` satisfies `x+yle800,` the line `x+y=800` together with the region containing `O(0,0)` represents `2x+yle1000.`
The y-axis and the region to its right-hand side represents `x ge0.`
The x-axis and the region above it represents `y ge0.`
Thus, hte shaded region represents the feasible region, whose vertices are P, Q, R, S, T and U.
Clearly, the coordinates of P and Q are (0,0) and (400,0) respectively.
On solving `x=400and 2x+y=1000,` we get `fR(400,200).`
On solving `x+y=800 and 2x+y=1000,` we get `A(200,600).`
On solving `y=700 and x+y=800,` we get `T(100,700).`
On solving `x=0 and and y=700,` we get `U(0,700).`
The values of `Z=4x+3y` at the points P, Q, R, S, T and E are respectively. `0,1600,2200,2600, 2500 and 2100.`
The maximum of these values is 2600 occurring at `S(200,600).`
`therefore` Z is maximum when `x=200and y=600.`
Thus, the company should make 200 belts of type A and 600 belts of type B to have a maximum profit.