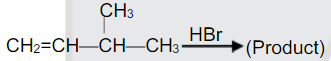A company produces three products every day. Their production on a certain day is 45 tons. It is found that the production of third product exceeds the production of first product by 8 tons while the total production of first and third product is twice the production of second product. Determine the production level of each product using matrix method.
To solve the problem using the matrix method, we will follow these steps:
Step 1: Define Variables
Let:
- x = production level of the first product (in tons)
- y = production level of the second product (in tons)
- z = production level of the third product (in tons)
Step 2: Formulate the Equations
From the problem statement, we can derive the following equations:
1. The total production of all three products is 45 tons:
x+y+z=45(Equation 1)
2. The production of the third product exceeds the production of the first product by 8 tons:
z−x=8⇒z=x+8(Equation 2)
3. The total production of the first and third products is twice the production of the second product:
x+z=2y⇒x+(x+8)=2y⇒2x+8=2y⇒x−y+4=0(Equation 3)
Step 3: Rewrite the Equations in Standard Form
We can rewrite the equations in standard form:
1. x+y+z=45
2. −x+z=8 (or −x+0y+z=8)
3. x−2y+z=0
Step 4: Set Up the Matrix Equation
We can express the system of equations in matrix form Ax=b:
⎡⎢⎣111−1011−21⎤⎥⎦⎡⎢⎣xyz⎤⎥⎦=⎡⎢⎣4580⎤⎥⎦
Step 5: Find the Inverse of Matrix A
First, we calculate the determinant of matrix A:
det(A)=1⋅(0⋅1−(−2)⋅1)−1⋅(−1⋅1−1⋅1)+1⋅(−1⋅(−2)−0⋅1)=1⋅(0+2)−1⋅(−1−1)+1⋅(2)=2+2+2=6
Next, we find the cofactors of matrix A and then the adjoint:
- The cofactor matrix C is:
⎡⎢⎣222−3031−21⎤⎥⎦
- The adjoint of A (transpose of the cofactor matrix) is:
adj(A)=⎡⎢⎣2−3120−2231⎤⎥⎦
Now, we can find the inverse of A:
A−1=1det(A)⋅adj(A)=16⎡⎢⎣2−3120−2231⎤⎥⎦
Step 6: Solve for x,y,z
Now we can find x by calculating A−1b:
x=A−1b=16⎡⎢⎣2−3120−2231⎤⎥⎦⎡⎢⎣4580⎤⎥⎦
Calculating the product:
1. First row: 2⋅45−3⋅8+1⋅0=90−24+0=66
2. Second row: 2⋅45+0⋅8−2⋅0=90+0−0=90
3. Third row: 2⋅45+3⋅8+1⋅0=90+24+0=114
Thus, we have:
x=16⎡⎢⎣6690114⎤⎥⎦=⎡⎢⎣111519⎤⎥⎦
Final Answer
The production levels are:
- x=11 tons (First Product)
- y=15 tons (Second Product)
- z=19 tons (Third Product)
Let:
- x = production level of the first product (in tons)
- y = production level of the second product (in tons)
- z = production level of the third product (in tons)
From the problem statement, we can derive the following equations:
1. The total production of all three products is 45 tons:
x+y+z=45(Equation 1)
2. The production of the third product exceeds the production of the first product by 8 tons:
z−x=8⇒z=x+8(Equation 2)
3. The total production of the first and third products is twice the production of the second product:
x+z=2y⇒x+(x+8)=2y⇒2x+8=2y⇒x−y+4=0(Equation 3)
We can rewrite the equations in standard form:
1. x+y+z=45
2. −x+z=8 (or −x+0y+z=8)
3. x−2y+z=0
We can express the system of equations in matrix form Ax=b:
⎡⎢⎣111−1011−21⎤⎥⎦⎡⎢⎣xyz⎤⎥⎦=⎡⎢⎣4580⎤⎥⎦
First, we calculate the determinant of matrix A:
det(A)=1⋅(0⋅1−(−2)⋅1)−1⋅(−1⋅1−1⋅1)+1⋅(−1⋅(−2)−0⋅1)=1⋅(0+2)−1⋅(−1−1)+1⋅(2)=2+2+2=6
- The cofactor matrix C is:
⎡⎢⎣222−3031−21⎤⎥⎦
- The adjoint of A (transpose of the cofactor matrix) is:
adj(A)=⎡⎢⎣2−3120−2231⎤⎥⎦
A−1=1det(A)⋅adj(A)=16⎡⎢⎣2−3120−2231⎤⎥⎦
Now we can find x by calculating A−1b:
x=A−1b=16⎡⎢⎣2−3120−2231⎤⎥⎦⎡⎢⎣4580⎤⎥⎦
1. First row: 2⋅45−3⋅8+1⋅0=90−24+0=66
2. Second row: 2⋅45+0⋅8−2⋅0=90+0−0=90
3. Third row: 2⋅45+3⋅8+1⋅0=90+24+0=114
x=16⎡⎢⎣6690114⎤⎥⎦=⎡⎢⎣111519⎤⎥⎦
The production levels are:
- x=11 tons (First Product)
- y=15 tons (Second Product)
- z=19 tons (Third Product)
Topper's Solved these Questions
Similar Questions
Knowledge Check
 Product , The product is :A
Product , The product is :A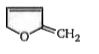 BHC=C−(CH2)3OnaCNaC=C−(CH2)3ONaDH−C=C−(CH2)3OH
BHC=C−(CH2)3OnaCNaC=C−(CH2)3ONaDH−C=C−(CH2)3OH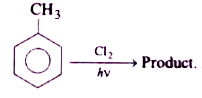 Product. Find correct product. A
Product. Find correct product. A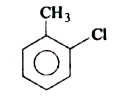 B
B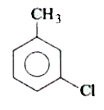 C
C D
D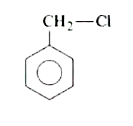
The first product of C4 pathway is
Aoxaloacetic acidBRuBPCPGADPGAL
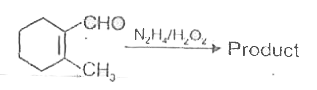
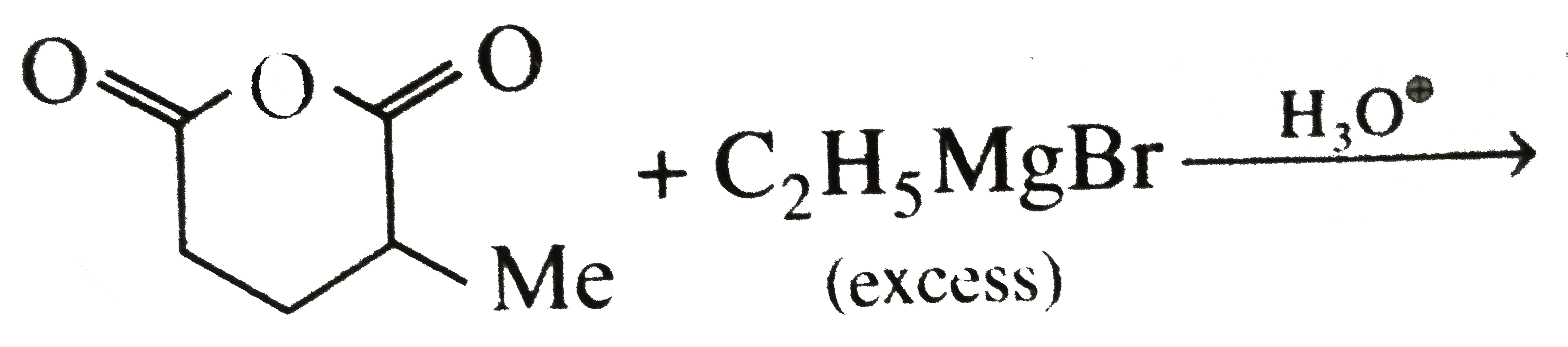 Product. The major product is :
Product. The major product is :
View SolutionThe final product / product mixture in the reaction sequence.

View SolutionDivide 28 into four parts in an A.P. so that the ratio of the product of first and third with the product of second and fourth is 8:15.
View SolutionDivide 28 into four parts in an A.P. so that the ratio of the product of first and third with the product of second and fourth is 8:15.
View SolutionChloral
 product. The product is :
product. The product is :
View Solution