A cumulative frequency distribution is given below. Convert this into a frequency distribution table. Marks Below 45 Below 60 Below 75 Below 90 Below 105 Below 120 No. of Students 0 8 23 48 85 116
To convert the given cumulative frequency distribution into a frequency distribution table, we will follow these steps:
Step 1: Understand the Cumulative Frequency
The cumulative frequency tells us how many students scored below a certain mark. For example, "Below 45" means 0 students scored below 45, "Below 60" means 8 students scored below 60, and so on.
Step 2: Identify Class Intervals
We will define the class intervals based on the cumulative frequency:
- Below 45: 0 to 45
- Below 60: 45 to 60
- Below 75: 60 to 75
- Below 90: 75 to 90
- Below 105: 90 to 105
- Below 120: 105 to 120
Step 3: Calculate the Frequencies
To find the frequency for each class interval, we subtract the cumulative frequency of the previous interval from the cumulative frequency of the current interval:
- For 0 to 45: Frequency = Cumulative frequency (Below 45) = 0
- For 45 to 60: Frequency = Cumulative frequency (Below 60) - Cumulative frequency (Below 45) = 8 - 0 = 8
- For 60 to 75: Frequency = Cumulative frequency (Below 75) - Cumulative frequency (Below 60) = 23 - 8 = 15
- For 75 to 90: Frequency = Cumulative frequency (Below 90) - Cumulative frequency (Below 75) = 48 - 23 = 25
- For 90 to 105: Frequency = Cumulative frequency (Below 105) - Cumulative frequency (Below 90) = 85 - 48 = 37
- For 105 to 120: Frequency = Cumulative frequency (Below 120) - Cumulative frequency (Below 105) = 116 - 85 = 31
Step 4: Construct the Frequency Distribution Table
Now we can organize this information into a frequency distribution table:
| Class Interval | Cumulative Frequency | Frequency |
|----------------|----------------------|-----------|
| 0 to 45 | 0 | 0 |
| 45 to 60 | 8 | 8 |
| 60 to 75 | 23 | 15 |
| 75 to 90 | 48 | 25 |
| 90 to 105 | 85 | 37 |
| 105 to 120 | 116 | 31 |
Final Answer
The frequency distribution table is as follows:
| Class Interval | Frequency |
|----------------|-----------|
| 0 to 45 | 0 |
| 45 to 60 | 8 |
| 60 to 75 | 15 |
| 75 to 90 | 25 |
| 90 to 105 | 37 |
| 105 to 120 | 31 |
The cumulative frequency tells us how many students scored below a certain mark. For example, "Below 45" means 0 students scored below 45, "Below 60" means 8 students scored below 60, and so on.
We will define the class intervals based on the cumulative frequency:
- Below 45: 0 to 45
- Below 60: 45 to 60
- Below 75: 60 to 75
- Below 90: 75 to 90
- Below 105: 90 to 105
- Below 120: 105 to 120
To find the frequency for each class interval, we subtract the cumulative frequency of the previous interval from the cumulative frequency of the current interval:
- For 0 to 45: Frequency = Cumulative frequency (Below 45) = 0
- For 45 to 60: Frequency = Cumulative frequency (Below 60) - Cumulative frequency (Below 45) = 8 - 0 = 8
- For 60 to 75: Frequency = Cumulative frequency (Below 75) - Cumulative frequency (Below 60) = 23 - 8 = 15
- For 75 to 90: Frequency = Cumulative frequency (Below 90) - Cumulative frequency (Below 75) = 48 - 23 = 25
- For 90 to 105: Frequency = Cumulative frequency (Below 105) - Cumulative frequency (Below 90) = 85 - 48 = 37
- For 105 to 120: Frequency = Cumulative frequency (Below 120) - Cumulative frequency (Below 105) = 116 - 85 = 31
Now we can organize this information into a frequency distribution table:
|----------------|----------------------|-----------|
| 0 to 45 | 0 | 0 |
| 45 to 60 | 8 | 8 |
| 60 to 75 | 23 | 15 |
| 75 to 90 | 48 | 25 |
| 90 to 105 | 85 | 37 |
| 105 to 120 | 116 | 31 |
The frequency distribution table is as follows:
|----------------|-----------|
| 0 to 45 | 0 |
| 45 to 60 | 8 |
| 60 to 75 | 15 |
| 75 to 90 | 25 |
| 90 to 105 | 37 |
| 105 to 120 | 31 |
Topper's Solved these Questions
Similar Questions
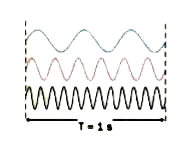
Find the frequency of the waves given below.
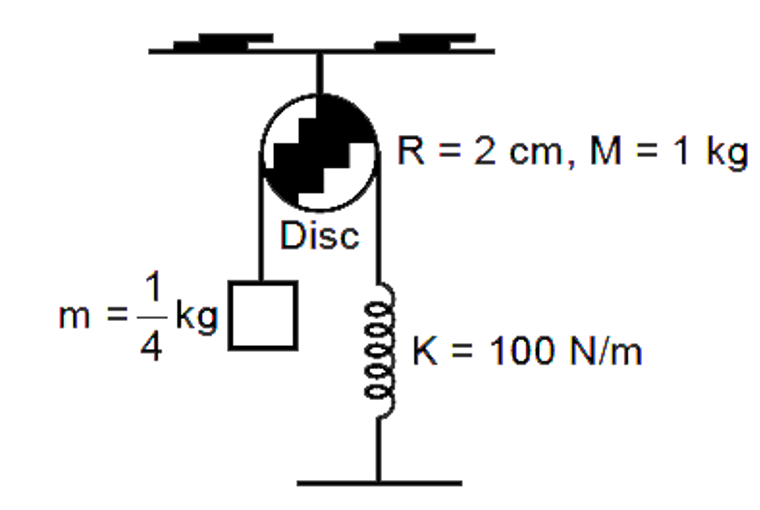
View SolutionFor the system given below, find the angular frequency of oscillation?
View SolutionComplexes given below show:

View SolutionComplexes given below show:

View SolutionCalculate the mean of the distribution given below using the short cut method.

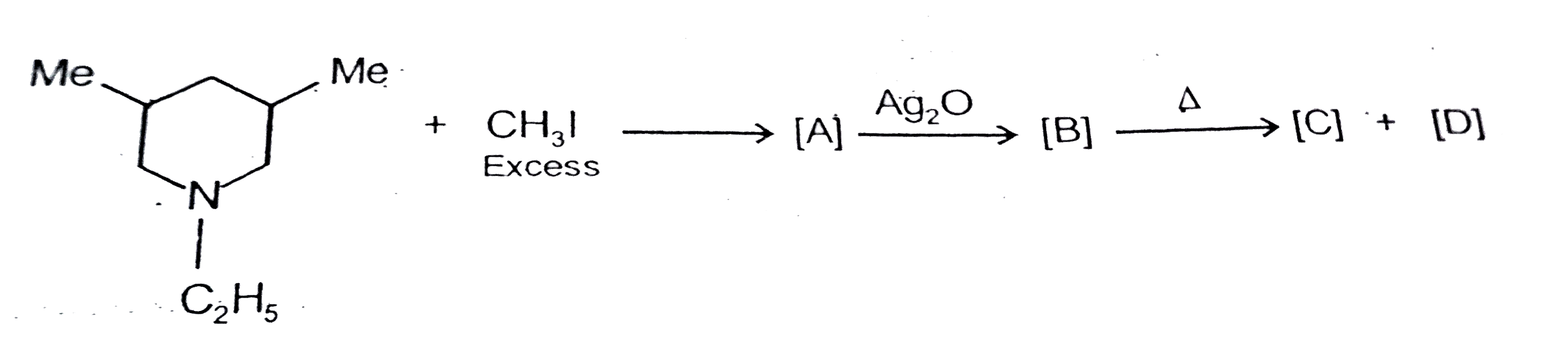
View SolutionComplete the reactions given below:
View SolutionThe structure given below is known as

View SolutionThe structure given below is known as
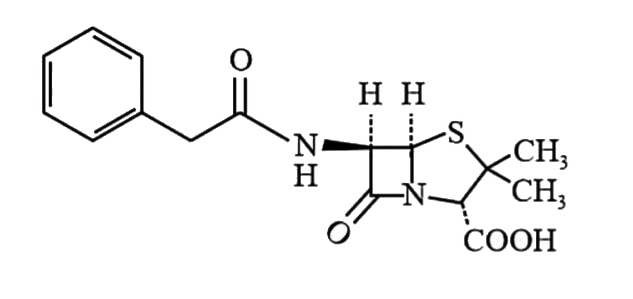
View SolutionThe structure given below is known as

View SolutionThe product of the reaction given below is
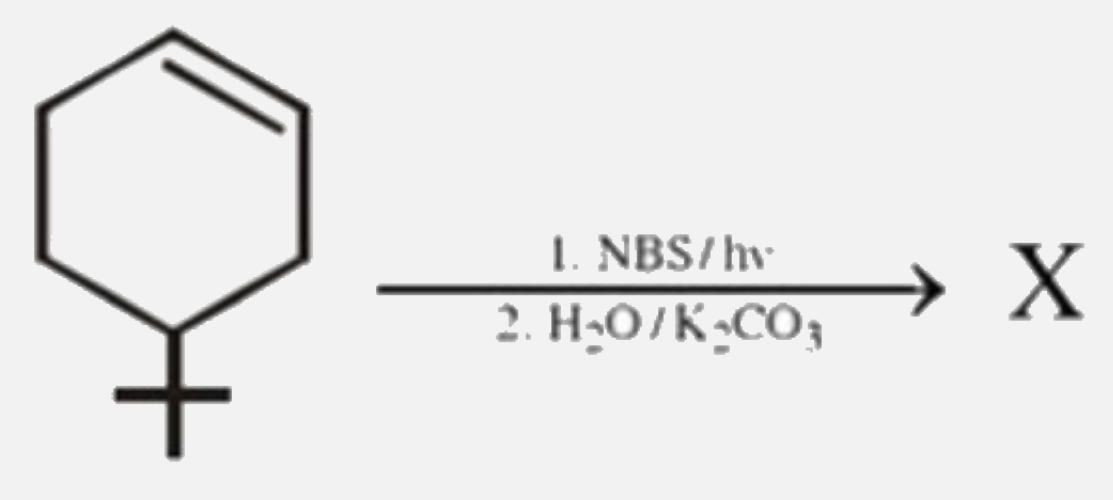
View Solution
