A diameter divides the circle into k equal halves. Then find the value of k..
The correct Answer is:2
To solve the question, "A diameter divides the circle into k equal halves. Then find the value of k," we can follow these steps:
1. Understanding the Circle and Diameter:
- A circle is a round shape with all points on its boundary equidistant from its center.
- A diameter is a line segment that passes through the center of the circle and has its endpoints on the circle's boundary.
2. Visualizing the Circle:
- Draw a circle and label its center as point O.
- Mark two points on the boundary of the circle, A and B, such that the line segment AB is the diameter.
3. Dividing the Circle:
- The diameter AB divides the circle into two distinct regions: the upper half and the lower half.
- These two regions are equal in area.
4. Determining the Value of k:
- Since the diameter divides the circle into two equal parts, we can conclude that k, which represents the number of equal halves, is equal to 2.
5. Final Answer:
- Therefore, the value of k is 2.
Conclusion:
The diameter of a circle divides it into 2 equal halves. Thus, the value of k is 2.
- A circle is a round shape with all points on its boundary equidistant from its center.
- A diameter is a line segment that passes through the center of the circle and has its endpoints on the circle's boundary.
- Draw a circle and label its center as point O.
- Mark two points on the boundary of the circle, A and B, such that the line segment AB is the diameter.
- The diameter AB divides the circle into two distinct regions: the upper half and the lower half.
- These two regions are equal in area.
- Since the diameter divides the circle into two equal parts, we can conclude that k, which represents the number of equal halves, is equal to 2.
- Therefore, the value of k is 2.
The diameter of a circle divides it into 2 equal halves. Thus, the value of k is 2.
Topper's Solved these Questions
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - OLYMPIAD/HOTS CORNER
10 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - SUBJECTIVE PROBLEMS(LONG ANSWER TYPE)
25 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- DATA HANDLING BOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLING EXERCISE - Olympiad/HOTS Corner
10 Videos
Similar Questions
If the area bounded by the curve x=y2 and the line x=4 gets divided by the line x=a into two equal halves, then find the value of a.
View SolutionConsider a circle with the X and Y axes as tangents to it in the first quadrant.If the line x+3y=8 passes through the center of the circle and the radius of the circle equals k, then find the value of 3k
View Solution
Knowledge Check
x2+hxy+y2−6x−2y+k=0 is the equation of the circle and 2 is the radius of the circle, then find the values of h and k ?
Ah=0,k=−6Bh=0,k=6Ch=−3,k=6Dh=3,k=6If the ordinate and abscissa of the point (k, 2 k - 1) be equal then the value of k is
A0B−1C1D12
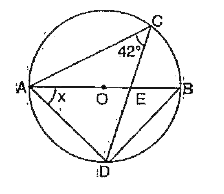
In the given circle with diameter AB find the value of x.
View SolutionA solid sphere of diameter 14 cm is cut into two equal halves. Find the increase in the total surface area of solid sphere?
View SolutionIf k,k+1,k+3 are in G.P then find the value of k
View SolutionIf k, k + 1 and k + 3 are in G.P. then find the value of k.
View SolutionThe area A of a parallel plate capacitor is divided into two equal, halves and filled with two media of dielectric constants K1andK2 respectively. The capacitance of the capacitor will be

View SolutionFind the ratio in which the point (-3, k) divides the join of A(-5, -4) and B(-2, 3). Also, find the value of k.
View Solution
