A die has its six faces marked 0,1,1,1,6,6. Two such dice are thrown together and the total is recorded.
(i) How many different scores are possible
(ii) What is the probability of getting a total of 7 ?
To solve the problem step by step, we will address both parts of the question: finding the different scores possible when two dice are thrown and calculating the probability of getting a total of 7.
Step 1: Identify the possible outcomes for one die
The faces of the die are marked as follows: 0, 1, 1, 1, 6, 6.
Thus, the possible outcomes when one die is thrown are:
- 0
- 1
- 1
- 1
- 6
- 6
Step 2: List the outcomes when two dice are thrown
When two dice are thrown, we can combine the outcomes from each die. We will consider all combinations of the outcomes from the first die with the outcomes from the second die.
Step 3: Calculate the possible scores
Now, we will list all possible sums from the combinations of the two dice:
1. (0, 0) → 0 + 0 = 0
2. (0, 1) → 0 + 1 = 1
3. (0, 1) → 0 + 1 = 1 (another 1)
4. (0, 1) → 0 + 1 = 1 (another 1)
5. (0, 6) → 0 + 6 = 6
6. (1, 0) → 1 + 0 = 1
7. (1, 1) → 1 + 1 = 2
8. (1, 1) → 1 + 1 = 2 (another 1)
9. (1, 6) → 1 + 6 = 7
10. (6, 0) → 6 + 0 = 6
11. (6, 1) → 6 + 1 = 7
12. (6, 1) → 6 + 1 = 7 (another 1)
13. (6, 6) → 6 + 6 = 12
Step 4: Collect unique scores
From the combinations above, we can collect the unique scores:
- 0
- 1
- 2
- 6
- 7
- 12
Thus, the different scores possible are: 0, 1, 2, 6, 7, 12.
Step 5: Count the different scores
The total number of different scores possible is 6.
Step 6: Calculate the probability of getting a total of 7
To find the probability of getting a total of 7, we need to consider the combinations that yield this total:
1. (1, 6)
2. (6, 1)
Now, we will calculate the probability of each outcome:
- Probability of rolling a 6: There are 2 faces with 6 out of 6 total faces, so P(6)=26=13.
- Probability of rolling a 1: There are 3 faces with 1 out of 6 total faces, so P(1)=36=12.
Step 7: Combine probabilities for total of 7
The total probability of getting a score of 7 can be calculated by considering both combinations:
- Probability of (1, 6) = P(1)×P(6)=12×13=16
- Probability of (6, 1) = P(6)×P(1)=13×12=16
Adding these probabilities together gives:
P(7)=16+16=26=13
Final Answers
(i) The number of different scores possible is 6.
(ii) The probability of getting a total of 7 is 13.
The faces of the die are marked as follows: 0, 1, 1, 1, 6, 6.
Thus, the possible outcomes when one die is thrown are:
- 0
- 1
- 1
- 1
- 6
- 6
When two dice are thrown, we can combine the outcomes from each die. We will consider all combinations of the outcomes from the first die with the outcomes from the second die.
Now, we will list all possible sums from the combinations of the two dice:
2. (0, 1) → 0 + 1 = 1
3. (0, 1) → 0 + 1 = 1 (another 1)
4. (0, 1) → 0 + 1 = 1 (another 1)
5. (0, 6) → 0 + 6 = 6
6. (1, 0) → 1 + 0 = 1
7. (1, 1) → 1 + 1 = 2
8. (1, 1) → 1 + 1 = 2 (another 1)
9. (1, 6) → 1 + 6 = 7
10. (6, 0) → 6 + 0 = 6
11. (6, 1) → 6 + 1 = 7
12. (6, 1) → 6 + 1 = 7 (another 1)
13. (6, 6) → 6 + 6 = 12
From the combinations above, we can collect the unique scores:
- 0
- 1
- 2
- 6
- 7
- 12
The total number of different scores possible is 6.
To find the probability of getting a total of 7, we need to consider the combinations that yield this total:
1. (1, 6)
2. (6, 1)
- Probability of rolling a 6: There are 2 faces with 6 out of 6 total faces, so P(6)=26=13.
- Probability of rolling a 1: There are 3 faces with 1 out of 6 total faces, so P(1)=36=12.
The total probability of getting a score of 7 can be calculated by considering both combinations:
- Probability of (1, 6) = P(1)×P(6)=12×13=16
- Probability of (6, 1) = P(6)×P(1)=13×12=16
P(7)=16+16=26=13
(i) The number of different scores possible is 6.
(ii) The probability of getting a total of 7 is 13.
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS
14 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWERS QUESTIONS
14 Videos
- REAL NUMBERSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
A die is thrown. Find the probability of getting: a number greater than 6 is 1.
View SolutionTwo dice are thrown together. Find the probability that the product the number on the top of the dice is
(i) 6 (ii) 12 (iii) 7
View SolutionA pair of dice is thrown 6 times. If getting a total of 7 is considered a success, what is the probability of at least 5 successes .
View SolutionA pair of dice is thrown 7 times. If getting a total of 7 is considered a success, what is the probability of atmost 6 success?
View SolutionA child has die whose six faces show the letters as given below:
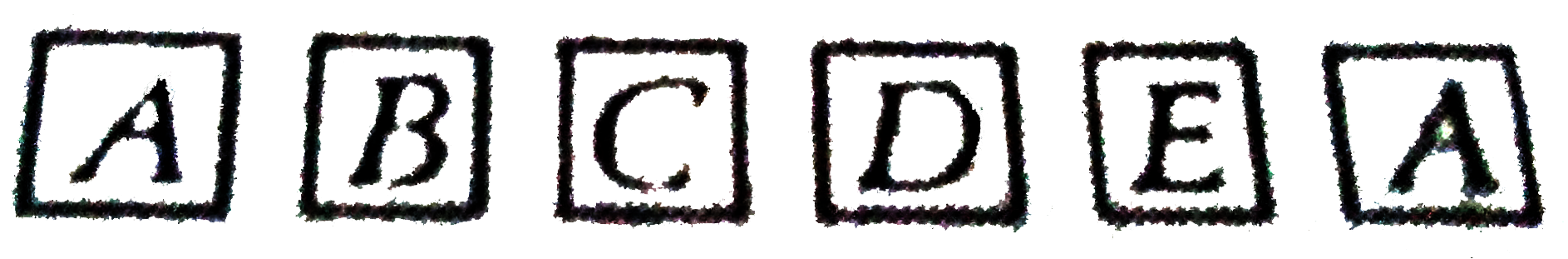
The die is thrown once. What is the probability of getting (i) A, (ii) D?
View SolutionA die has 6 faces marked by the given numbers as shown below :

The die is thrown once. What is the probability of getting
(i) a positive integer.
View SolutionA dice has 6 faces marked by the given below :
1, 2, 3, -1, -2, -3
The dice is thrown once. What is the probability of getting an integer greater than −3?
View SolutionA dice has 6 faces marked by the given below :
1, 2, 3, -1, -2, -3
The dice is thrown once. What is the probability of getting a positive integer?
View SolutionA die has 6 faces marked by the given numbers as shown below :

The die is thrown once. What is the probability of getting
(iii) the smallest integer.
View SolutionA child has a die whose 6 faces show the letter as given below: A,B,C,A,A,B. The die is thrown once. What is the probability of getting (i) A (ii) B
View Solution
