A die is thrown once. If probabililty of an event X is denoted by P(X), find:
a. (i) P (even number)
(ii) P(a number ≥3)
) (iii) P (a number between 2 and 5)
b. (i) P (a number ≥4)
(ii) P(a number <7)
(iii) P (a number >6).
The correct Answer is:a. (i) 12 (ii) 23 (iii) 13 (b) (i) 23 (ii) 1 (iii) 0
To solve the problem, we will analyze the outcomes of throwing a die and calculate the probabilities for the specified events.
1. Identify the Sample Space:
The sample space when a die is thrown consists of the numbers {1, 2, 3, 4, 5, 6}. This gives us a total of 6 possible outcomes.
2. Calculate P(even number):
- The even numbers in the sample space are {2, 4, 6}.
- Number of favorable outcomes = 3 (even numbers).
- Total outcomes = 6.
- Probability, P(even number) = Number of favorable outcomes / Total outcomes = 3 / 6 = 1 / 2.
3. Calculate P(a number ≥ 3):
- The numbers greater than or equal to 3 in the sample space are {3, 4, 5, 6}.
- Number of favorable outcomes = 4.
- Total outcomes = 6.
- Probability, P(a number ≥ 3) = 4 / 6 = 2 / 3.
4. Calculate P(a number between 2 and 5):
- The numbers between 2 and 5 (exclusive) are {3, 4}.
- Number of favorable outcomes = 2.
- Total outcomes = 6.
- Probability, P(a number between 2 and 5) = 2 / 6 = 1 / 3.
5. Calculate P(a number ≥ 4):
- The numbers greater than or equal to 4 are {4, 5, 6}.
- Number of favorable outcomes = 3.
- Total outcomes = 6.
- Probability, P(a number ≥ 4) = 3 / 6 = 1 / 2.
6. Calculate P(a number < 7):
- All numbers in the sample space {1, 2, 3, 4, 5, 6} are less than 7.
- Number of favorable outcomes = 6.
- Total outcomes = 6.
- Probability, P(a number < 7) = 6 / 6 = 1.
7. Calculate P(a number > 6):
- There are no numbers in the sample space that are greater than 6.
- Number of favorable outcomes = 0.
- Total outcomes = 6.
- Probability, P(a number > 6) = 0 / 6 = 0.
Final Answers:
a.
(i) P(even number) = 1/2
(ii) P(a number ≥ 3) = 2/3
(iii) P(a number between 2 and 5) = 1/3
b.
(i) P(a number ≥ 4) = 1/2
(ii) P(a number < 7) = 1
(iii) P(a number > 6) = 0
The sample space when a die is thrown consists of the numbers {1, 2, 3, 4, 5, 6}. This gives us a total of 6 possible outcomes.
- The even numbers in the sample space are {2, 4, 6}.
- Number of favorable outcomes = 3 (even numbers).
- Total outcomes = 6.
- Probability, P(even number) = Number of favorable outcomes / Total outcomes = 3 / 6 = 1 / 2.
- The numbers greater than or equal to 3 in the sample space are {3, 4, 5, 6}.
- Number of favorable outcomes = 4.
- Total outcomes = 6.
- Probability, P(a number ≥ 3) = 4 / 6 = 2 / 3.
- The numbers between 2 and 5 (exclusive) are {3, 4}.
- Number of favorable outcomes = 2.
- Total outcomes = 6.
- Probability, P(a number between 2 and 5) = 2 / 6 = 1 / 3.
- The numbers greater than or equal to 4 are {4, 5, 6}.
- Number of favorable outcomes = 3.
- Total outcomes = 6.
- Probability, P(a number ≥ 4) = 3 / 6 = 1 / 2.
- All numbers in the sample space {1, 2, 3, 4, 5, 6} are less than 7.
- Number of favorable outcomes = 6.
- Total outcomes = 6.
- Probability, P(a number < 7) = 6 / 6 = 1.
- There are no numbers in the sample space that are greater than 6.
- Number of favorable outcomes = 0.
- Total outcomes = 6.
- Probability, P(a number > 6) = 0 / 6 = 0.
a.
(i) P(even number) = 1/2
(ii) P(a number ≥ 3) = 2/3
(iii) P(a number between 2 and 5) = 1/3
(i) P(a number ≥ 4) = 1/2
(ii) P(a number < 7) = 1
(iii) P(a number > 6) = 0
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE 16 (C ) LONG ANSWER TYPE QUESTIONS -II LATQ3videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE 16 (D ) SHORT ANSWER TYPE QUESTIONS SATQ9videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE 16 (C ) SHORT ANSWER TYPE QUESTIONS SATQ9videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - CHAPTER TEST12videos
PERMUTATIONS AND COMBINATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Chapter Test11videos
RELATIONS AND FUNCTIONS
Similar Questions
A die is thrown once. Find the probability of getting
(i) an even number (ii) a number less than 5
(iii) a number greater than 2 (iv) a number between 3 and 6
(v) a number other than 3 (vi) the number 5 .View SolutionA die is thrown. Find the probability of getting: (i) an even prime number (ii) a number greater than 5 (iii) a number lying between 2 and 6
View SolutionA die is thrown once. Find the probability of getting a number which (i) is a prime number (ii) lies between 2 and 6.
View SolutionA die is thrown once. Find the probability of getting(i) a prime number; (ii) a number lying between 2 and 6; (iii) an odd number.
View SolutionA die is thrown once. Find the probabilty of getting:
(i) an odd number (ii) a number between 2 and 6.View SolutionIn a single throw of a die, find the probability of getting.
(i) a prime number
(ii) an even number
(iii) an even prime numberView SolutionIn a single throw of a die find the probability that the number :
(i) will be an even number (ii) will not be an even number
(iii) will be an odd number.View SolutionIn a single throw of two dice, find
(i) P (an odd number on the first die and a 6 on the second)
(ii) P (a number greater than 3 on each die)
(iii) P (a total of 10)
(iv) P (a total greater than 8)
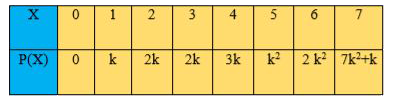
(v) P (a total of 9 or 11)View SolutionA random variable X has the following probability distribution:
Determine : (i) k (ii) P(X<3) (iii) P(X>4)View SolutionA die is rolled, A is the event of getting (i) a prime number (ii) a number less than 5. Write event A, n(A), P(A).
View Solution

