A diet is to contain at leat 80 units of vitamin A and 100 units of minerals. Two foods $F_{1}$ and $F_{2}$ are available. Food $F_{1}$ cost Rs. 4 per unit and $F_{2}$ costs Rs. 6 per unit. One unit of food $F_{1}$ contains 3 units of vitamin A and 4 units of minerals. One unit of food $F_{2}$ contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.

Video Solution

Text Solution

Verified by Experts

Let $x$ units of $F_{1}$ and $y$ units of $F_{2}$ be in the food. Then,

Maximise $Z = 4 x + 6 y$ …………….1
Constraints $3 x + 6 y \geq 80$ ………………….2
$4 x + 3 y \geq 100$ ……………….3
$x \geq 0, y \geq 0$ …………………..4
First, draw the graph of the line $3 x + 6 y = 80$ ,.

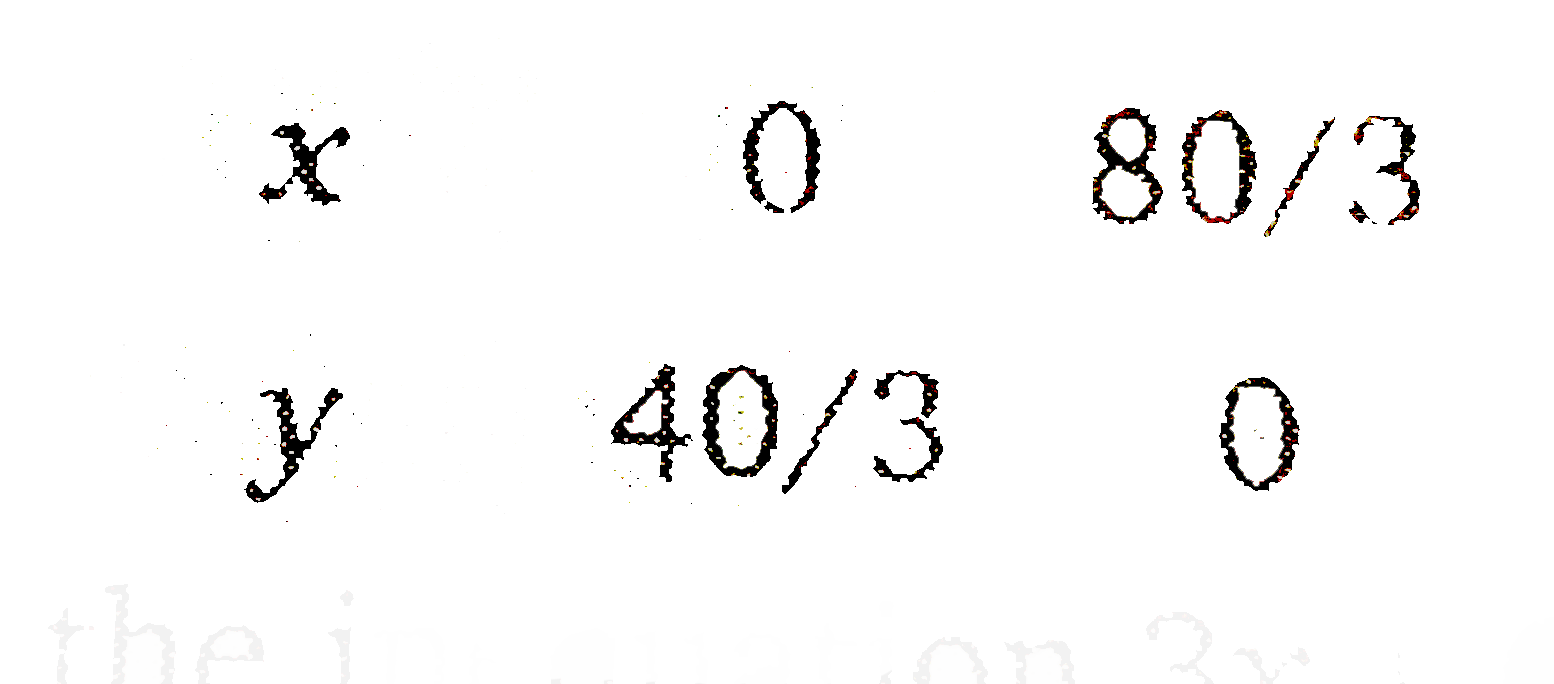
Put $(0, 0)$ in the inequation $3 x + 6 y \geq 80$ ,
$3 \times 0 + 6 \times 0 \geq 80 \Rightarrow 0 \geq 80$ (False)
Thus, the half plane does not contain the origin.
Since $x, y \geq 0$ so the feasible solution is in the first quadrant.
Now, draw the graph of the line $4 x + 3 y = 100$

Put $(0, 0)$ in the inequation $4 x + 3 y \geq 100$ ,
$4 \times 0 + 3 \times 0 \geq 100$
$\Rightarrow 0 \geq 100$ (False)
Thus, the half plane does not contain the origin.
From equations $3 x + 6 y = 80$ and $4 x + 3 y = 100$ . The point of intersection is $B (24, \frac{4}{3})$
Clearly, the feasible region is unbounded.
The vertices the feasible region are $A (\frac{80}{3}, 0), B (24, \frac{4}{3})$ and $C (0, \frac{100}{3})$ . We find the value of $Z$ at these vertices.

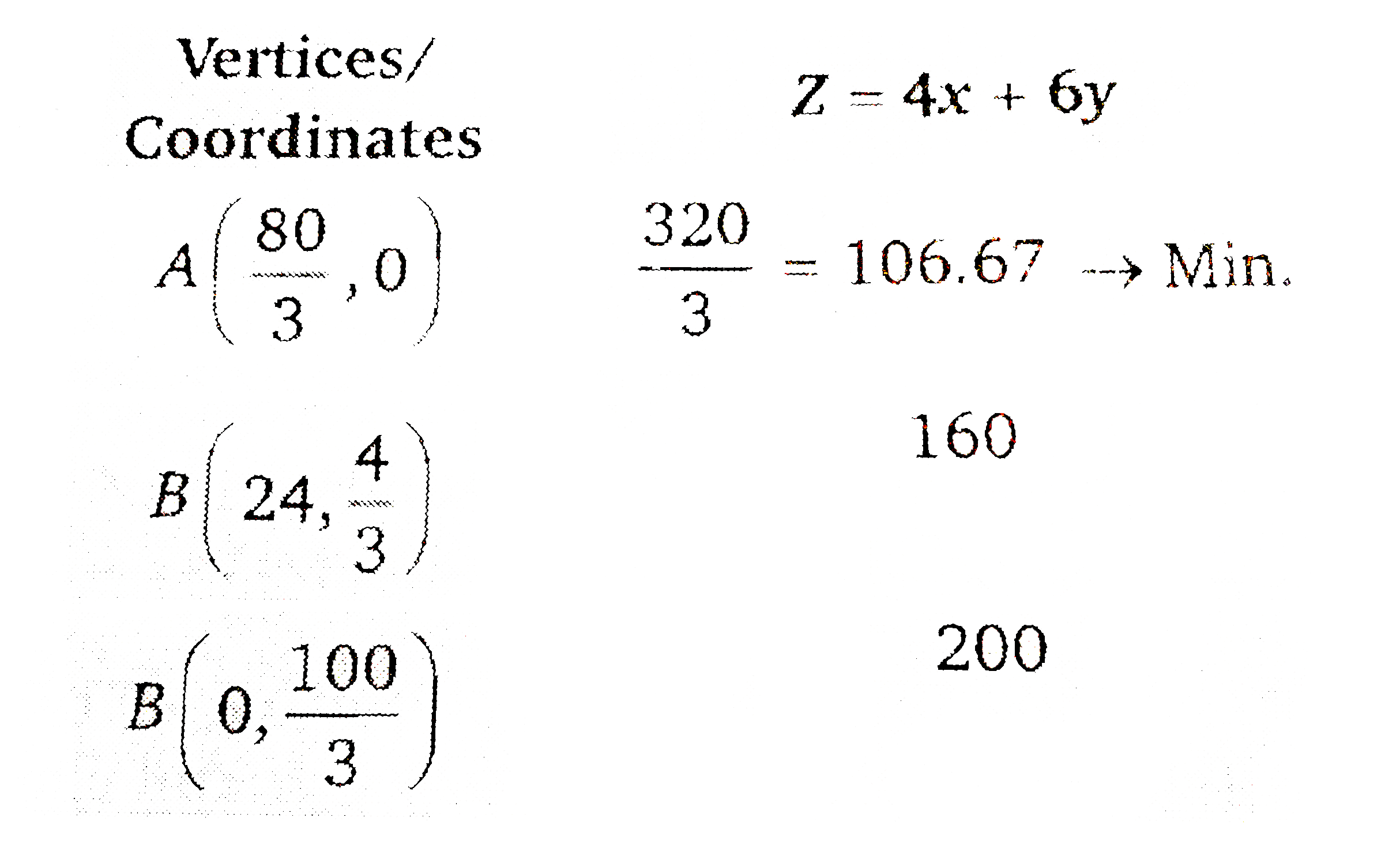
Since the feasible region is unbounded, so the minimum value of $z$ may or may not be 104. For this we draw the graph of inequations $4 x + 6 t < 104$ or $2 x + 3 y < 52$ . There is no common point here, so the minimum cost of mixture is Rs. 104.

|

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-LINEAR PROGRAMMING-Exercise 12.2

Home
Ask Doubt
Profile