A distribution consists of three components with frequencies 45, 40 and 15 having their means 2, 2.5 and 2, respectively. The mean of the combined. distribution is
220
2.2
100
45
The correct Answer is:B
To find the mean of the combined distribution, we can use the formula for the combined mean of different groups. The combined mean Cm is given by:
Cm=∑(fi⋅mi)∑fi
where:
- fi is the frequency of the ith component,
- mi is the mean of the ith component.
Step 1: Identify the frequencies and means
We have three components with the following frequencies and means:
- For the first component: f1=45, m1=2
- For the second component: f2=40, m2=2.5
- For the third component: f3=15, m3=2
Step 2: Calculate the weighted sum of the means
Now we calculate fi⋅mi for each component:
- For the first component: f1⋅m1=45⋅2=90
- For the second component: f2⋅m2=40⋅2.5=100
- For the third component: f3⋅m3=15⋅2=30
Step 3: Sum the products
Now, we sum these products:
∑(fi⋅mi)=90+100+30=220
Step 4: Sum the frequencies
Next, we sum the frequencies:
∑fi=45+40+15=100
Step 5: Calculate the combined mean
Now we can calculate the combined mean Cm:
Cm=∑(fi⋅mi)∑fi=220100=2.2
Final Answer
The mean of the combined distribution is 2.2.
---
- fi is the frequency of the ith component,
- mi is the mean of the ith component.
We have three components with the following frequencies and means:
- For the first component: f1=45, m1=2
- For the second component: f2=40, m2=2.5
- For the third component: f3=15, m3=2
Now we calculate fi⋅mi for each component:
- For the first component: f1⋅m1=45⋅2=90
- For the second component: f2⋅m2=40⋅2.5=100
- For the third component: f3⋅m3=15⋅2=30
Now, we sum these products:
∑(fi⋅mi)=90+100+30=220
Next, we sum the frequencies:
∑fi=45+40+15=100
Now we can calculate the combined mean Cm:
Cm=∑(fi⋅mi)∑fi=220100=2.2
The mean of the combined distribution is 2.2.
Topper's Solved these Questions
- STATISTICSBOOK - ARIHANT PUBLICATION BIHARCHAPTER - STATISTICSEXERCISE - EXAM BOOSTER (FOR CRACKING EXAM)
25 Videos
- SIMPLE INTEREST AND COMPOUND INTEREST BOOK - ARIHANT PUBLICATION BIHARCHAPTER - SIMPLE INTEREST AND COMPOUND INTEREST EXERCISE - Exam Booster for Cracking Exam
25 Videos
- TAXATIONBOOK - ARIHANT PUBLICATION BIHARCHAPTER - TAXATIONEXERCISE - EXAM BOOSTER FOR CRACKING EXAM
14 Videos
Similar Questions
Knowledge Check
The distribution consists of three components with frequencies 45 , 40 and 15 having their means 2,2.5 and 2 respectively . The mean of the combined distribution is
A220B2.2C100D45(x + 2), x and (x - 1) are the frequencies of the numbers 12, 15 and 20 respectively. If the mean of the distribution is 14.5, the value of x is
A2B3C4D5Let a distribution be made by combining three distribution each having mean zero standard deviations, each having mean zero, standard deviations 3,4 and 5 respectively. Then the variance of the combined distribution is equal to
A26615B17C503D6215
Find the mean of the following frequency distribution:

View SolutionFind the mean of the followings frequency distribution :

View SolutionCompute the mean (M) from the frequency distribution
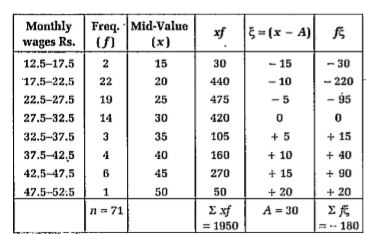
View SolutionFind the mean for the following frequency distribution :
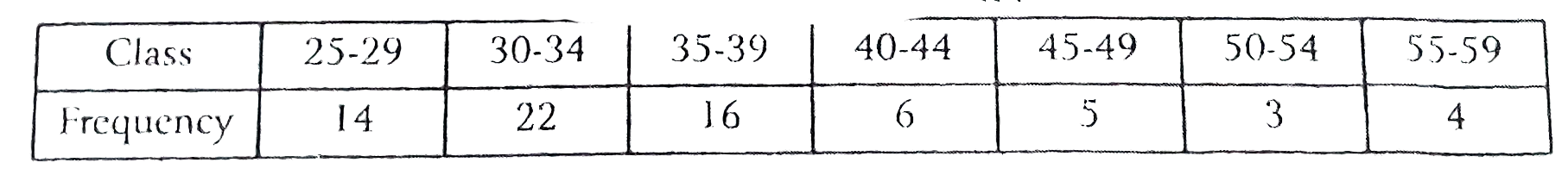
View SolutionArithmetic mean of a continuous frequency distribution
View Solution


