A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of sc
Let the manufacturer makes x packets of screw A and y packets of screw B per day. Then

Maximise Z=7x+10y………………1
and constraints
4x+6y≤240⇒2x+3y≤120…………………2
6x+3y≤240⇒2x+y≤80.....................3
and x≥0,y≥0
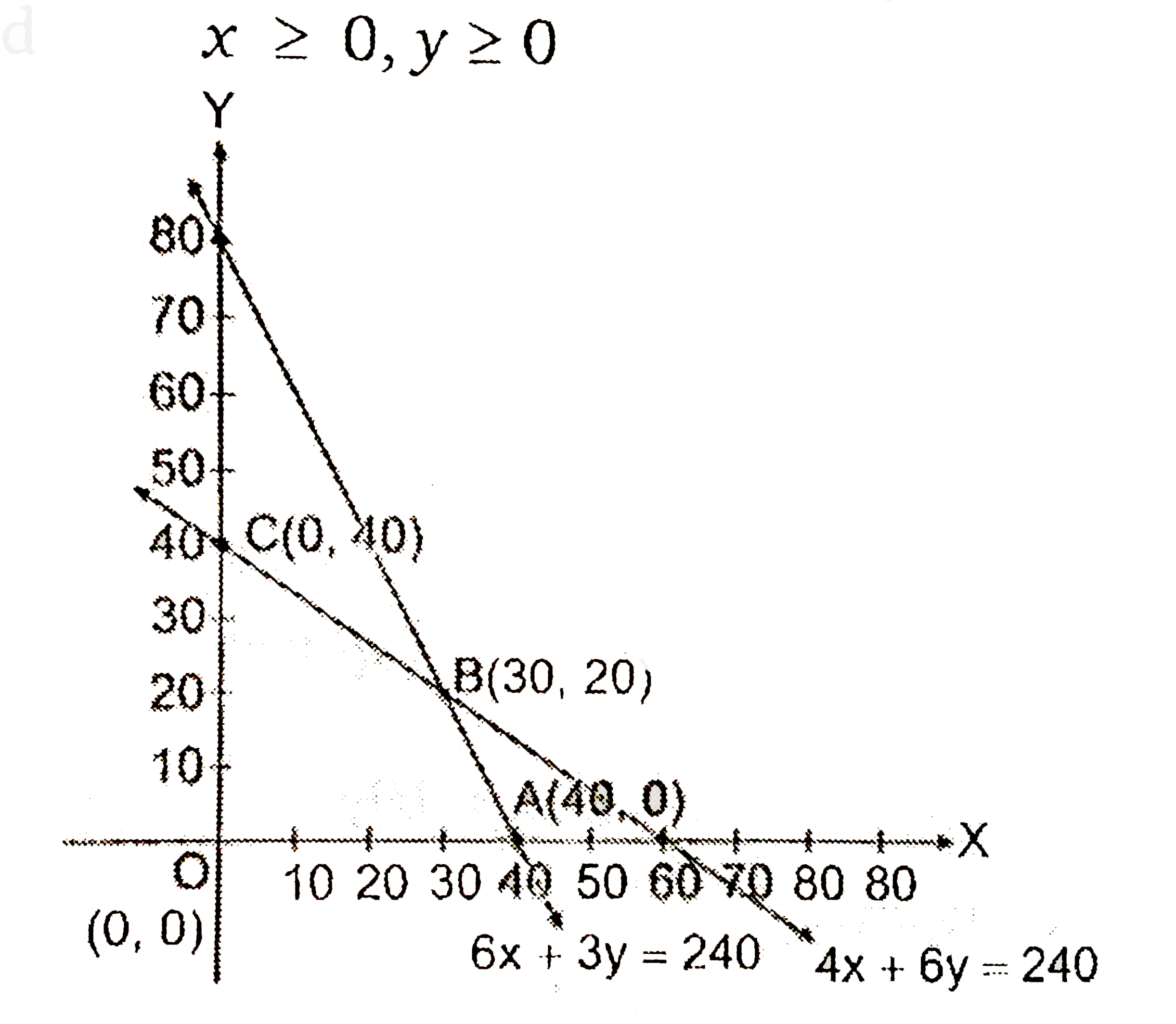
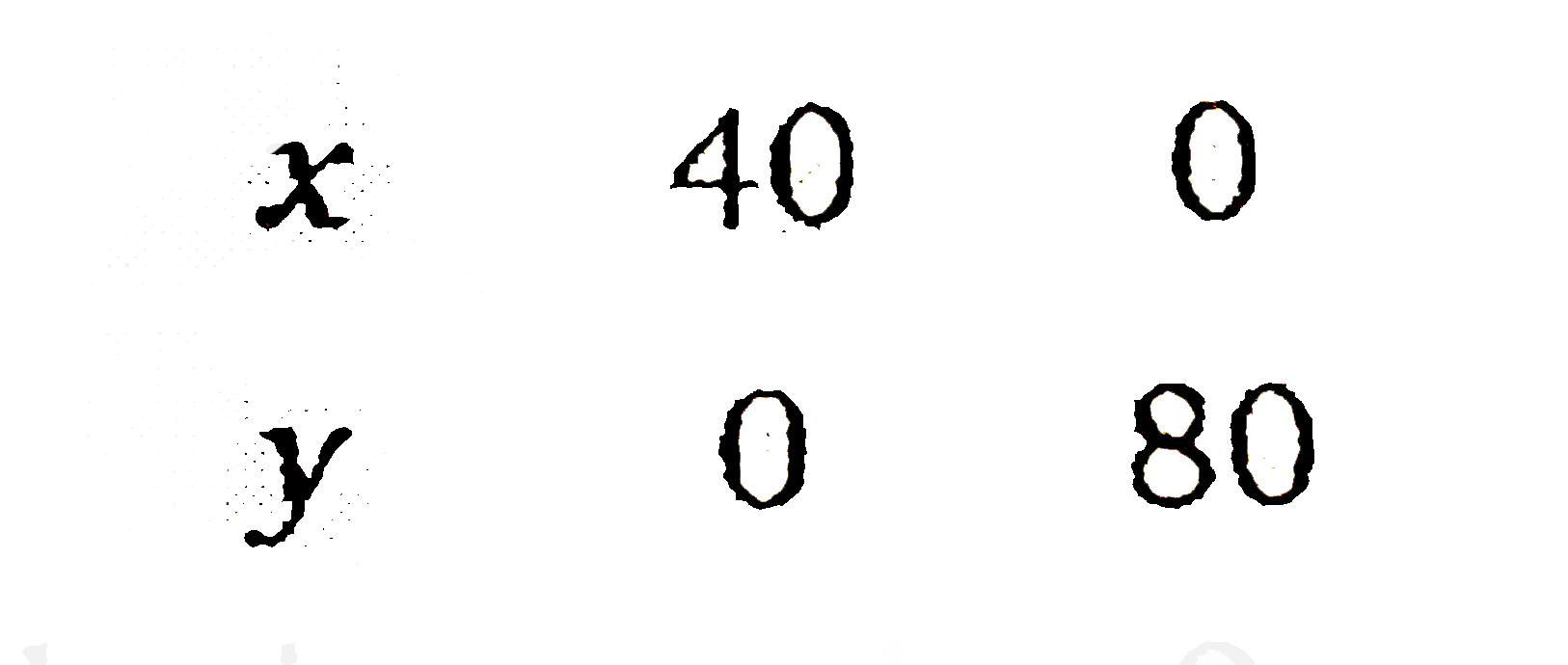
First draw the graph of the line 2x+3y=120
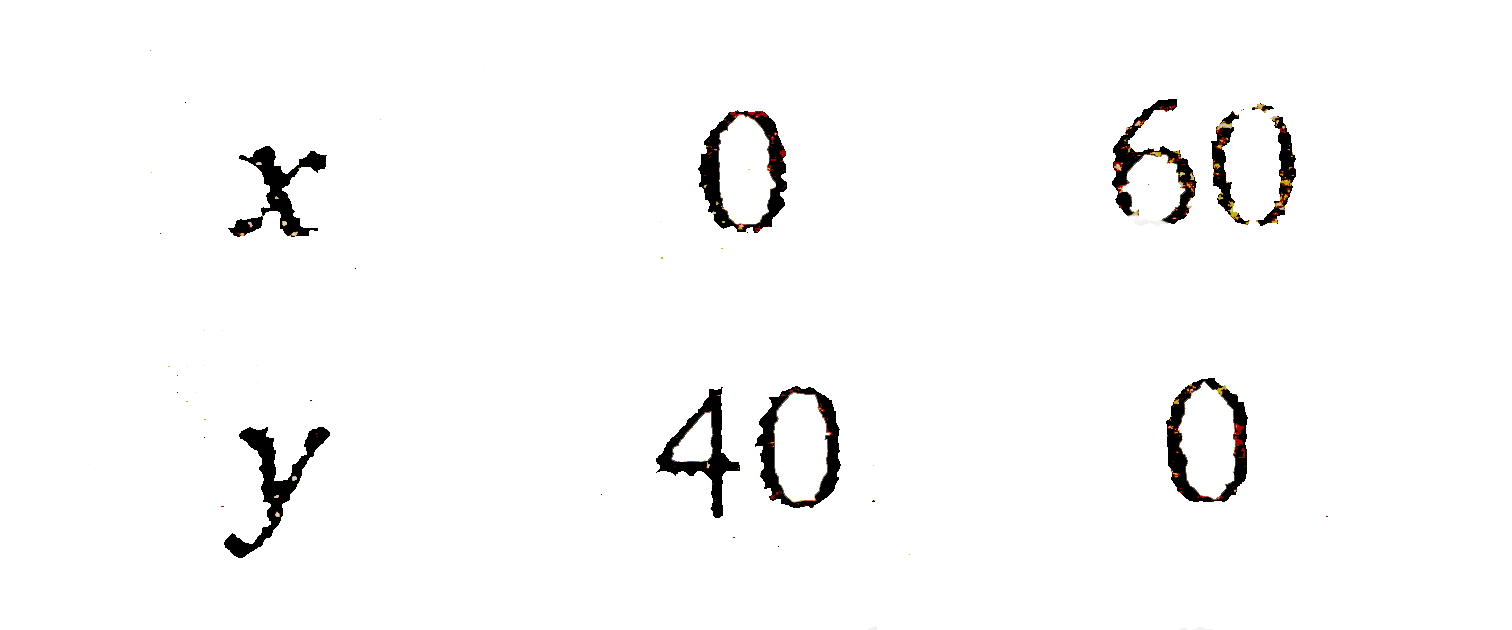
Put (0,0) in the inequation 2x+3y≤120
2×0+3×0≤120
⇒0≤120 (True)
Therefore, half plane contains the origin,
Now draw the graph of the line 2x+y=80
Put (0,0) in the inequation 2x+y≤80
2×0+0≤80⇒0≤80 (True)
Therefore half plane contains the origin.Since, x,y≥0. So the feasible region will be in first quadrant.
From equations 2x+3y=120 and 2x+y=80 the point of intersection is B(30,20).
∴ Feasible region is OABCE.
The vertices of the feasible region are O(0,0),A(40,0),B(30,20) and C(0,40) we find the value of Z at these points.
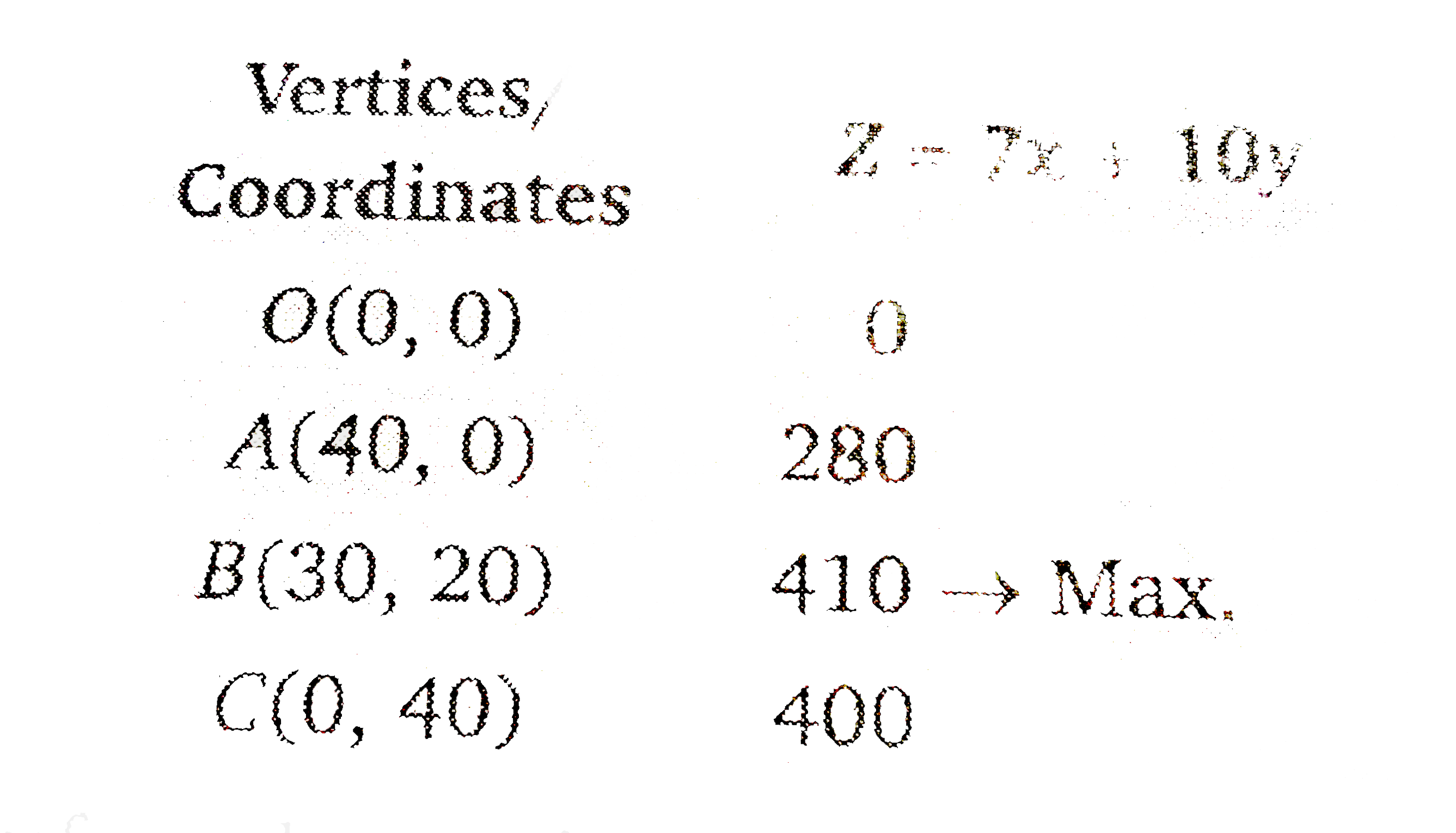
Therefore, the maximum value of Z is Rs. 410 at point B(30,20). Therefore, the maximum profit of Rs. 410 will be obtained when the factory produces 30 packets of screw A and 20 packets of screw B per day.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise
9 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.1
10 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
A factory manufactures two types of screws, A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on hand-operated machines to manufacture a packet of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machines to manufacture a packet of screws 'B'. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a packet of screws 'A' at a profit of 70 paise and screws 'B' at a profit of Rs. 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximise his profit ? Formulate the above L.P.P. and solve it graphically and find the maximum profit.
View SolutionA company manufactures two types of screws A and B. all the screws have to pass through a threading machine and a slotting machine. A box of type A screw requires 2min on the threading machine and 3 min on the slotting machine. A box of type B screw requires 8 min on the threading machine and 2 min on the slotting machine. In a week each machine is availbale for 60h. On selling these screws, the company gets a profit of 100 box on type A screw and 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
View SolutionA company manufactures two types of toys A and B. A toy of type A requires 5 minute for cutting and 10 minute for assembling. A toy of type B requires 8 minute for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling th etoys in a day. The profit is Rs 50 each on a toy of Type A and Rs 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit ? Use linear programming to find the solution.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionManufacturer produces two types of steel trunks. He has two machines, A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 per trunk on the first type of trunk and Rs. 25 per trunk on the second type. Formulate a linear programming problem to find out how many trunks of each type he must make each day to maximize his profit.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 25 and that from a shade is Rs. 15. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit. Formulate an LPP and solve it graphically.
View SolutionA factory owner purchases two types of machines, A and B, for his factory. The requirements and limitations for the machines are as follows:

He has an area of 7600 sq. m available and 72 skilled men who can operate the machines. To find how many machines of each type should he buy to maximize the daily output, formulate this as a L.P.P.
View SolutionA company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is Rs. 40 on each unit of product of type A and Rs. 50 on each unit of type B. How many units of each type should the company manufacture so as to earn maximum profit ? Use linear programming to find the solution.
View SolutionA manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea cups. The time in minutes required for manufacturing each cup on the machines is given below:
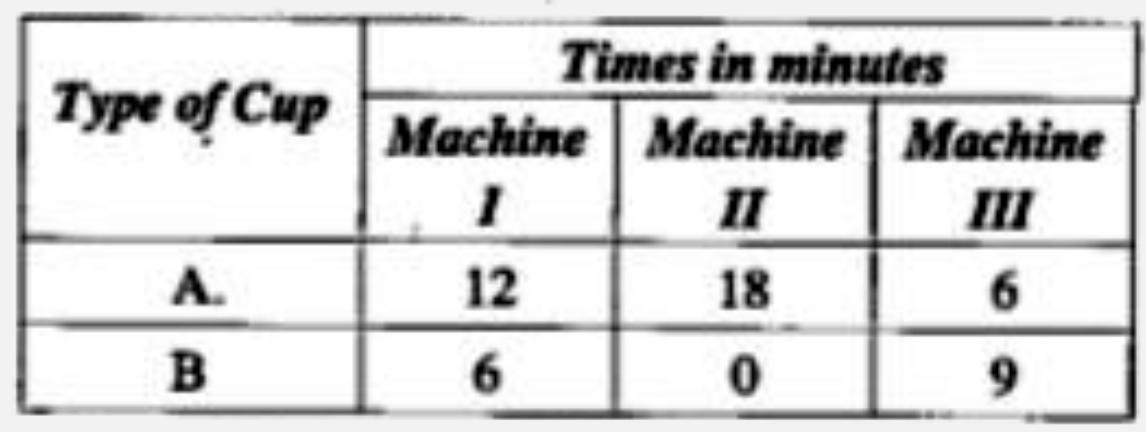
Each machine is available for a maximum of six hours per day. If the profit on each cup of type A is Rs 1.50and that'on each cup of type B is Rs 1.00, find the number of cups of each type that should be manufactured in a day to get maximumprofit.
View Solution
