A faniture dealer deals in only two itmes - tables and chairs. He has 'Rs. 50000 invest and has storage place of at most 60 pieces. A table costs Rs. 2500 and chair Rs. 500. He estimates that from the sale of one table, he can make a perfect Rs. 250 and that from the sale of one chair a profit of Rs. 75. How many table and chair he should buy from the available money so as to maximise his total profit assuming that he can sell all the items which he buys.
This problem can be formulated as under.
Let x and y be the required numbers of tables and chairs reprectively. Then, clearly we have
x≥0,y≥0,x+y≤60,
250x+50y≤5000,i.e.,5x+y≤100.
Let P be the profit function. Then, P=50x+15y. Now, we have to maximize. P
Now, x+y=60⇒x60+y60=1.
This line meets the axes at (60,0)and?(0,60). Plot these points and join them to get the line x+y=60.
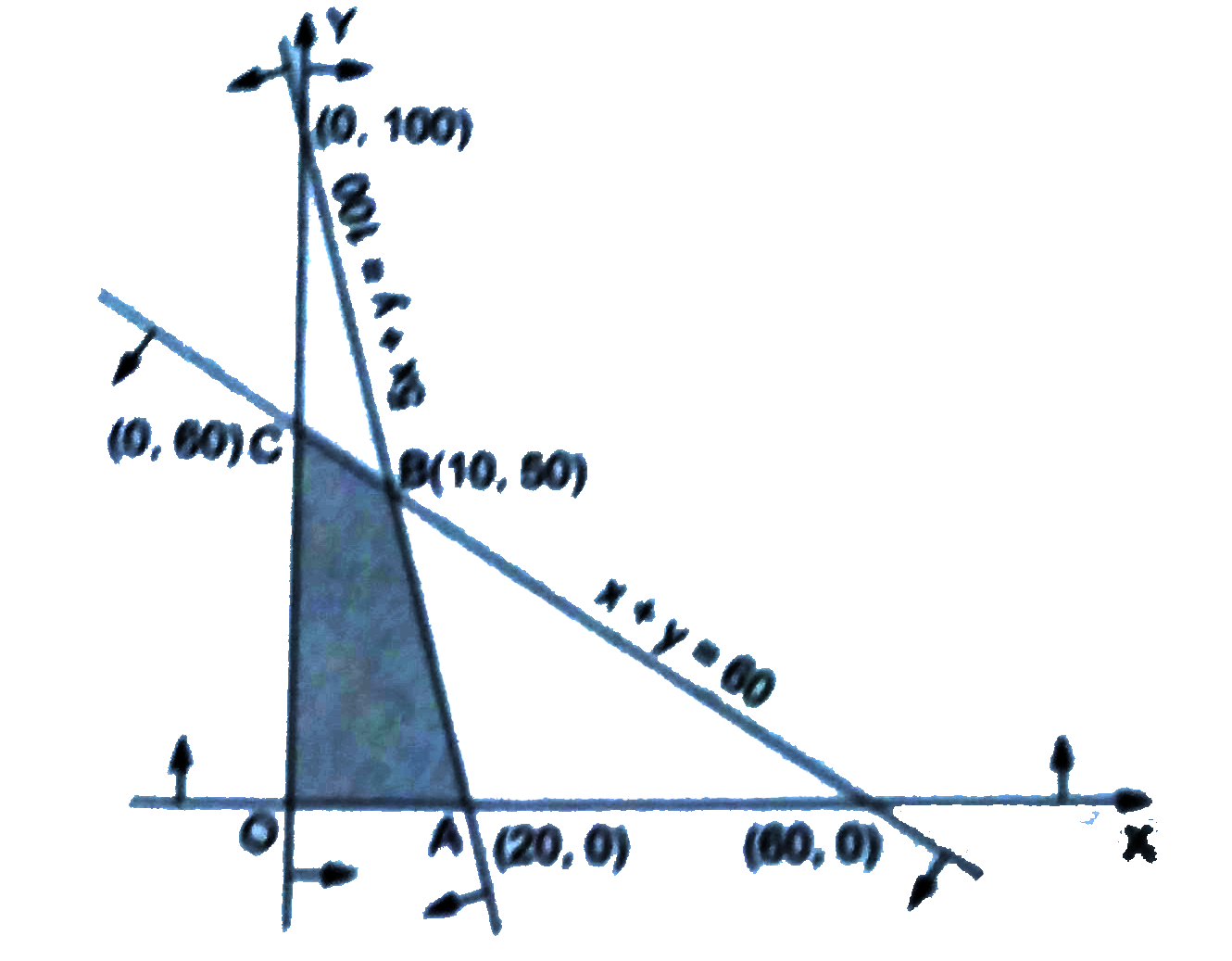
Also, 5x+y=100⇒x20+y100=1.
This line meets the axes at (20,0)and(0,100). Plot these points and join them to get the line 5x+y=100.
Also, the line x=0 is the y-axis and the line y=0is teh x-axis. These foru straight line enclose the quadrilateral OABC. The conordinates of the points O,A,B,Care(0,0),(20,0),(10,50),and(6,60) respectively.
At these points, the corresponding values of P=50x+15yare0,100,1250and900 respectively.
Clearly, it is maximum at B(10,50).
So, for a maximum profit, the dealer should purchase 10 tables and 50 chairs.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exprcise 33A
11 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exprcise 33B
38 Videos
- LINEAR DIFFERENTIAL EQUATIONS BOOK - RS AGGARWALCHAPTER - LINEAR DIFFERENTIAL EQUATIONS EXERCISE - Objective Questions
27 Videos
- MATRICESBOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5F
21 Videos
Similar Questions
Knowledge Check
A furniture deals in only two items -tables and chairs, He has 50000 to invest and has storage space of atmost 60 pieces. A table costs 2500 and a chair costs 500. Then, the constraints of the above problem are (where, x is number of tables and y is number of chairs)
Ax≥,0y≥0B5x+y≤100Cx+y≤60DAll of theseA furniture dealer deals in only two items namely tables and chairs. He has Rs. 5000 to invest and space to store at most 60 pieces. A table cost him Rs. 250 and a chair Rs. 60. He can sell a table at a profit of Rs. 15. Assume that he can sell all the items that he produced. The number of constraints in the problem are
A2B3C4D5If a furniture dealer estimate that from the sale of one table he can make a profit of ₹ 250 and from the sale of one chair of a profit of ₹ 75 and if x is the sale of chairs and y us the number of tables , then its linear objectives function is
AZ= 75 x + 250 yBZ=75x + 25 YCZ = 250 + 75 yDZ = 25 x + 75 y
4 chairs and 3 tables cost Rs. 2100 and 5 chairs and 2 tables cost Rs. 1750. find the cost of one chair and one table separately.
View Solution2 tables and 3 chairs together cost Rs 2000 whereas 3 tables and 2 chairs together cost Rs 2500. Find the total cost of 1 table and 5 chairs
View SolutionA furniture dealer deals in only items - tables and chairs. He has ₹15,000 to invest and a space to store atmost 60 pieces. A table costs him ₹750 and chair ₹150 . Suppose he makes x tables any y chairs
The graphical solution of the inequations representing given data is
View SolutionTwo chain and three tables cost Rs. 1025 and three chairs and two tables cost Rs. 1100. What is the difference between the cost of one table and that of one chair?
View SolutionA dealer wishes to purchase table fans and ceiling fans. He has Rs. 57,600 to invest, and has space to store 40 items. A table fan costs Rs. 750 and ceiling fan costs Rs. 900. He can make profits of Rs. 70 and Rs. 90 by selling a table fan and a ceiling fan respectively. If dealer sell all the fans that he buy, the formulate this problem as LPP, to maximize the profit.
View Solution