A farmer F1 has a land in the shape of a triangle with vertices at P(0,0),Q(1,1) and R(2,0).From this land, a neighbouring farmer F2 takes away the region which lies between the side PQ and a curve of the form y=xn,(n>1). If the area of the region taken away by the farmer F2 is exactly 30% of the area of ΔPQR, then the value of n is _______.
The correct Answer is:4
Step by step video & image solution for A farmer F_1 has a land in the shape of a triangle with vertices at P(0, 0), Q(1, 1) and R(2, 0).From this land, a neighbouring farmer F_2 takes away the region which lies between the side PQ and a curve of the form y=x^n, (n gt1). If the area of the region taken away by the farmer F_2 is exactly 30% of the area of DeltaPQR, then the value of n is _______. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A farmer F1 has a land in the shape of a triangle with vertices at P(0, 0), Q(1, 1)and R(2, 0) . From this land, a neighbouring farmer F2 takes away the region which lies between the side PQ and a curve of the form y=xn (n>1) . If the area of the region taken away by the farmer F2 is exactly 30% of the area of △PQR , then the value of n is _______.
View SolutionLet (5+2√6)n=p+f, where n∈Nandp∈Nand0<f<1, then the value of f2−f+pf−p is
View Solution
Knowledge Check
The slope of the tangent to a cruve y=f(x) at (x,f(x)0 is 2x+1.If the curve passes through the point (1,2) then the area of the region bounded by the curve,the x-axis and the lien x=1 is
A56 sq. unitsB65 sq.unitsC16 sq. unitsD6 sq. unitsFor r>0,f(r) is the ratio of perimeter to area of a circle of radius r. Then f(1) + f(2) is equal to
A1B2C3D4The area of the region bounded by curves y=1−x2,x+y+1=0andx−y−1=0 is
A103B73C83D3
Let f(x) be a function which satisfy the equation f(xy)=f(x)+f(y) for all x>0,y>0 such that f'(1)=2. Find the area of the region bounded by the curves y=f(x),y=∣∣x3−6x2+11x−6∣∣andx=0.
View SolutionLet F1(x1,0) and F2(x2,0), for x1<0 and x2>0, be the foci of the ellipse x29+y28=1 Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant. If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of area of the triangle MQR to area of the quadrilateral MF1NF2 is
View SolutionLet F1(x1,0) and F2(x2,0), for x1<0 andx2>0, be the foci of the ellipse x29+y28=1. Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant.
If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of the area of the triangle MQR to area of the quadrilateral MF1NF2 is :
View SolutionIf A(n) represent the area bounded by the curve y=n lnx (where n∈N and n>1) and x-axis from x=1 to x=e, then value of A(n)+nA(n−1) is equal to
View SolutionThe given bar graph represents the producution and sales of a certain crop in quintals by the farmers F1, F2 , F3 and F4 .
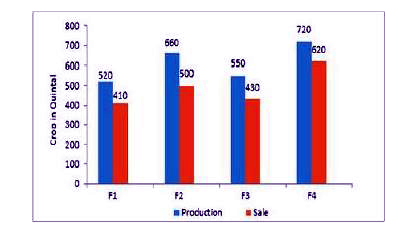
Which farmers recorded the highest percentage of sales with respect to the production ?
View Solution