A field is in the shape of a trapezium having parallel sides 90 m and 30 m.
These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough 1 m2 of the field, find the total cost of ploughing the field.
To solve the problem step by step, we will follow these steps:
Step 1: Identify the dimensions of the trapezium
The trapezium has two parallel sides:
- AB = 90 m (longer parallel side)
- CD = 30 m (shorter parallel side)
The other two sides are:
- AD = 100 m (the non-parallel side)
- BC = height (which we need to find)
Step 2: Find the height of the trapezium
Since the sides AB and CD meet the third side AD at right angles, we can form a right triangle using the height (BC) and the difference in lengths of the parallel sides.
The length of BE (the horizontal distance from point B to line CD) can be calculated as:
BE=AB−CD=90m−30m=60m
Now, we can apply the Pythagorean theorem in triangle ABE:
AD2=AB2+BE2
Substituting the known values:
1002=h2+602
This simplifies to:
10000=h2+3600
Now, isolate h2:
h2=10000−3600=6400
Taking the square root gives:
h=√6400=80m
Step 3: Calculate the area of the trapezium
The area A of a trapezium can be calculated using the formula:
A=12×(AB+CD)×h
Substituting the known values:
A=12×(90+30)×80
Calculating the sum of the parallel sides:
A=12×120×80
Calculating the area:
A=96002=4800m2
Step 4: Calculate the total cost of ploughing the field
The cost to plough 1 m² of the field is Rs 4. Therefore, the total cost C to plough the entire area is:
C=Area×Cost per m2
Substituting the values:
C=4800×4
Calculating the total cost:
C=19200Rs
Final Answer
The total cost of ploughing the field is Rs 19200.
---
The trapezium has two parallel sides:
- AB = 90 m (longer parallel side)
- CD = 30 m (shorter parallel side)
- AD = 100 m (the non-parallel side)
- BC = height (which we need to find)
Since the sides AB and CD meet the third side AD at right angles, we can form a right triangle using the height (BC) and the difference in lengths of the parallel sides.
BE=AB−CD=90m−30m=60m
AD2=AB2+BE2
Substituting the known values:
1002=h2+602
This simplifies to:
10000=h2+3600
Now, isolate h2:
h2=10000−3600=6400
Taking the square root gives:
h=√6400=80m
The area A of a trapezium can be calculated using the formula:
A=12×(AB+CD)×h
Substituting the known values:
A=12×(90+30)×80
Calculating the sum of the parallel sides:
A=12×120×80
Calculating the area:
A=96002=4800m2
The cost to plough 1 m² of the field is Rs 4. Therefore, the total cost C to plough the entire area is:
C=Area×Cost per m2
Substituting the values:
C=4800×4
Calculating the total cost:
C=19200Rs
The total cost of ploughing the field is Rs 19200.
Topper's Solved these Questions
- HERON'S FORMULABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Short Answer Type Questions
10 Videos
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.4 Long Answer Type Questions
5 Videos
- INTRODUCTION TO EUCLID GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.4 Long Answer Type Questions
5 Videos
Similar Questions
A field is in the shape of a trapezium whose parallel sides are 25m and 10 m. The non-parallel sides are 14m and 13m. Find the area of the field.
View SolutionA field is in the shape of a trapezium whose parallel sides are 25m and 10 m. The non-parallel sides are 14m and 13m. Find the area of the field.
View SolutionFind the area of a trapezium whose parallel sides 25cm,13cm and other sides are 15cmand15cm
View SolutionIf the area of a trapezium is 28cm2 and one of its parallel sides is 6cm, find the other parallel side if its altitude is 4cm.
View SolutionA field is in the shape of a parallelogram. The two adjacent sides are in the ratio 4:5. A fence 216 m long is placed along the boundary of the field. Find the sides of the parallelogram.
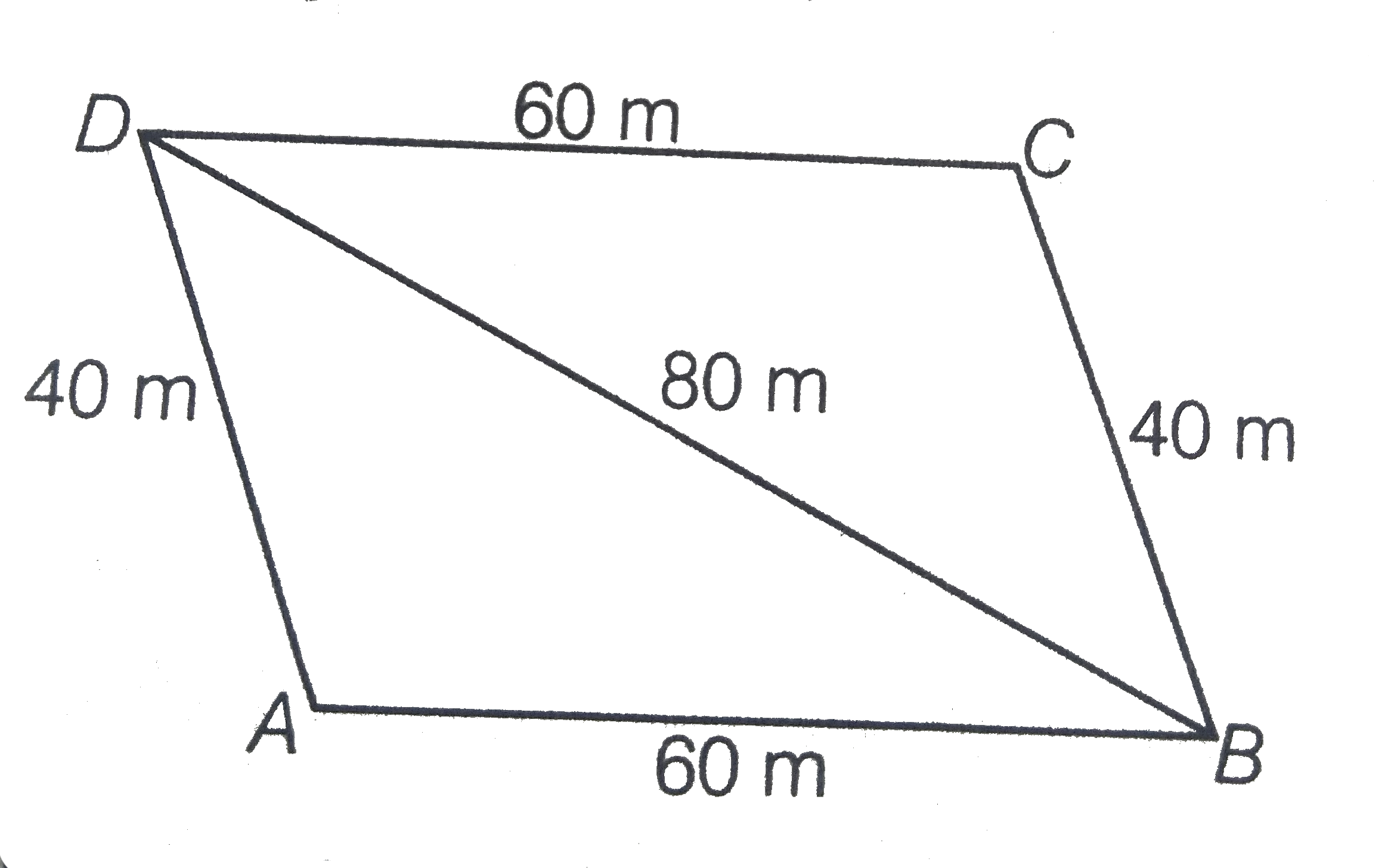
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
View SolutionThe cost of fencing a circular field at the rate of Rs 240 per metre is Rs 52,800. The field is to be ploughed at the rate of Rs 12.50 per m2. Find the cost of ploughing the field.
View SolutionThe cost of fencing a circular field at the rate of Rs. 240 per metre is Rs. 52,800. The field is to be ploughed at the rate of 12.50 per m2. Find the cost of ploughing the field.
View SolutionA field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40 m, DC = 50 m and angle A=90∘. Find the area of the field.
View Solutionthe hypotenuse of a right angle triangle is 1m less than twice the shortest side. If the third side is 1m more than the shortest side, find the sides of the triangle.
View Solution
