A figure consists of a semi-circle with a rectangle on its diameter. Given that the parameter of the figure is 20 feei. In order that its area may be maximum, its length and breadth are equal.
The correct Answer is:F
To solve the problem step by step, we will analyze the figure consisting of a semicircle with a rectangle on its diameter. We need to find the dimensions of the rectangle such that the area of the entire figure is maximized, given that the perimeter is 20 feet.
Step 1: Define the Variables
Let:
- R = radius of the semicircle
- L = length of the rectangle
- B = breadth of the rectangle
Since the rectangle is placed on the diameter of the semicircle, the breadth of the rectangle will be equal to the diameter of the semicircle, which is 2R.
Step 2: Write the Perimeter Equation
The perimeter P of the figure consists of the semicircle and the rectangle. The perimeter can be expressed as:
P=Length of semicircle+Length of rectangle+Length of rectangle
This can be written as:
P=12πR+2L+2R
Given that the perimeter is 20 feet, we have:
12πR+2L+2R=20
Step 3: Solve for L
Rearranging the equation to solve for L:
2L=20−12πR−2R
L=10−14πR−R
Step 4: Write the Area Function
The area A of the figure consists of the area of the semicircle and the area of the rectangle:
A=Area of semicircle+Area of rectangle
This can be expressed as:
A=12πR2+L⋅B
Substituting B=2R and the expression for L:
A=12πR2+(10−14πR−R)(2R)
A=12πR2+20R−12πR2−2R2
This simplifies to:
A=20R−2R2
Step 5: Maximize the Area
To find the maximum area, we take the derivative of A with respect to R and set it to zero:
dAdR=20−4R
Setting the derivative equal to zero:
20−4R=0⟹R=5
Step 6: Verify Maximum Area
To confirm that this is a maximum, we take the second derivative:
d2AdR2=−4
Since the second derivative is negative, this indicates that the area function has a maximum at R=5.
Step 7: Find Dimensions
Now, substituting R=5 back to find L:
L=10−14π(5)−5
Calculating L:
L=10−5π4−5=5−5π4
And the breadth B:
B=2R=10
Conclusion
Thus, the dimensions of the rectangle for maximum area are:
- Length L=5−5π4
- Breadth B=10
Let:
- R = radius of the semicircle
- L = length of the rectangle
- B = breadth of the rectangle
The perimeter P of the figure consists of the semicircle and the rectangle. The perimeter can be expressed as:
P=Length of semicircle+Length of rectangle+Length of rectangle
This can be written as:
P=12πR+2L+2R
Given that the perimeter is 20 feet, we have:
12πR+2L+2R=20
Rearranging the equation to solve for L:
2L=20−12πR−2R
L=10−14πR−R
The area A of the figure consists of the area of the semicircle and the area of the rectangle:
A=Area of semicircle+Area of rectangle
This can be expressed as:
A=12πR2+L⋅B
Substituting B=2R and the expression for L:
A=12πR2+(10−14πR−R)(2R)
A=12πR2+20R−12πR2−2R2
This simplifies to:
A=20R−2R2
To find the maximum area, we take the derivative of A with respect to R and set it to zero:
dAdR=20−4R
Setting the derivative equal to zero:
20−4R=0⟹R=5
To confirm that this is a maximum, we take the second derivative:
d2AdR2=−4
Since the second derivative is negative, this indicates that the area function has a maximum at R=5.
Now, substituting R=5 back to find L:
L=10−14π(5)−5
Calculating L:
L=10−5π4−5=5−5π4
And the breadth B:
B=2R=10
Thus, the dimensions of the rectangle for maximum area are:
- Length L=5−5π4
- Breadth B=10
Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - PROBLEM SET(3) (FILL IN THE BLANKS )
8 Videos
- MAXIMA AND MINIMA BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - SELF ASSESSMENT TEST
27 Videos
- MAXIMA AND MINIMA BOOK - ML KHANNACHAPTER - MAXIMA AND MINIMA EXERCISE - PROBLEM SET(3) (MULTIPLE CHOICE QUESTIONS)
15 Videos
- MATRICESBOOK - ML KHANNACHAPTER - MATRICESEXERCISE - COMPREHENSION
3 Videos
- MEASURES OF CENTRAL TENDENCY BOOK - ML KHANNACHAPTER - MEASURES OF CENTRAL TENDENCY EXERCISE - ASSERTION / REASON
1 Videos
Similar Questions
A figure consists of a semi-circle with a rectangle on its diameter. Given the perimeter of the figure, find its dimensions in order that the area may be maximum.
View SolutionThe figure shows a rectangle with its length and breadth as indicated.
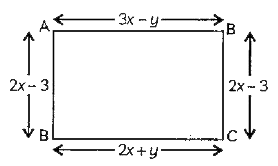
Given that the perimeter of the rectangle is 120cm, find:
the values of x and y
View SolutionThe perimeter of a rectangle is 36 m. Its length is 2 m greater than its breadth. Find its length and breadth.
View SolutionWhat will happen to the area of a rectangle if its length is doubled and breadth is trebled. its length and breadth are doubled?
View SolutionThe length of rectangle is three times its breadth. If the perimeter of the rectangle is 96 metres, then find the length and breadth of the rectangle.
View SolutionLength of a rectangle is three times its breadth and the perimeter of the rectangle is 40cm. Find its length and width.
View SolutionA rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.
View SolutionThe length of a rectangle exceeds its breadth by 6m if the perimeter of the rectangle is 84m, find its length and breadth
View SolutionThe perimeter of the given figure enclosed by a semi circle and a diameter is
View SolutionThe length of a rectangle is three times its breadth. If the perimeter of rectangle is 96 m, find the area of the rectangle.
View Solution
