A function whose graph is symmetrical in opposite quadrants is
A
f(x)=ex+e−x
B
f(x)=logex
C
f(x+y)=f(x)+f(y)
D
f(x)=cos(x)+sinx
Video Solution
Text Solution
The correct Answer is:C
We know that the graph of an odd function is symmetrical in opposite quadrants and the function satisfying the equation .
f(x+y)=f(x)+f(y) for all x,y∈R has the forumla
f(x)=xf(1) for all x∈R.
Clearly , it is an odd function . Hence, its graph is symmetrical in opposite quadrants.
|
Topper's Solved these Questions
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Section I - Solved Mcqs
95 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Section II - Assertion Reason Type
8 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- SCALAR AND VECTOR PRODUCTS OF THREE VECTORS BOOK - OBJECTIVE RD SHARMACHAPTER - SCALAR AND VECTOR PRODUCTS OF THREE VECTORS EXERCISE - Exercise
65 Videos
Similar Questions
Knowledge Check
A function whose graph is symmetrical about y-axis is
Af(x)=x(3x−13x−1)Bf(x)=log2(x+√x2+1)Cf(x+y)=f(x)+f(y)Df(x)=sinx+cosxWhich of the following is a function whose graph is symmetrical about the origin ?
Af(x)=(2x+2−x)Bf(x)=[log(x+√1+x2)]2Cf(x+y)=f(x)+f(y)∀x,y∈RDNone of theseSuppose R is relation whose graph is symmetric to both X-axis and Y-axis and that the point (1,2) is on the graph of R. Which one of the following is not necessarily on the graph of R?
A(-1,2)B(1,-2)C(-1,-2)D(2,1)
A function whose graph is symmetrical about the y axis is given by f(x)=sin[log(x+√x2+1)]
View SolutionArea of symmetrical graphs
View SolutionFunctions and Graphs
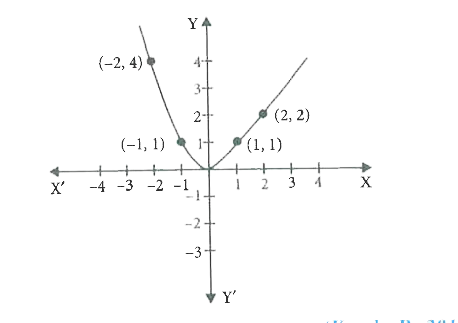
View SolutionWrite the function whose graph is shown below:
View SolutionFor the function g whose graph is given, state the value of each quantity, if it exists.
View Solution
