A functions from the set of natural numbers to integers defined by
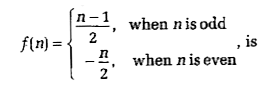
one-one but not onto
onto but not one-one
one-one and onto both
none of these
The correct Answer is:C
Step by step video, text & image solution for A functions from the set of natural numbers to integers defined by by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNCTIONSBOOK - ML KHANNACHAPTER - FUNCTIONSEXERCISE - COMPREHENSION
3 Videos
- EXPONENTIAL AND LOGARITHMIC SERIES BOOK - ML KHANNACHAPTER - EXPONENTIAL AND LOGARITHMIC SERIES EXERCISE - Problem Set (2) (Self Assessment Test)
8 Videos
- HEIGHTS AND DISTANCESBOOK - ML KHANNACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Problem Set (3) FILL IN THE BLANKS
9 Videos
Similar Questions
A function f from the set of natural numbers to integers is defined by n when n is odd f(n) 3, when n is even Then f is (b) one-one but not onto a) neither one-one nor onto (c) onto but not one-one (d) one-one and onto both
View SolutionA function R on the set N of natural numbers is defined as R={[2n,2n+1]:n∈N}
The domain of R …
View Solution
Knowledge Check
A function f from the set of natural number to integers defined by
f(n)={n−12when n is odd−n2when n is evenAneither one-one nor ontoBone-one but not ontoCone but not one-oneDone-one and onto bothIf f be a function from the set of natural numbers to the set of even natural numbers given by f(x) = 2x. Then, f is:
AOne-one but not ontoBOnto but not one-oneCBoth one-one and ontoDNeither one-one nor ontoLet f be a function from the set of natural numbers to the set of even natural numbers given by f(x)=2x. Then f is
Aone to one but not ontoBonto but not one-oneCboth one-one and ontoDneither one-one nor onto
Let f be a one - to - one function from the set of natural number to itself such that f(mn) = f(m) f (n) for all natural numbers m and n. What is the least possible value f (999) ?
View SolutionThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
View SolutionThe function f:N→N,N being the set of of natural numbers, defined by f(x)=2x+3 is
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View SolutionThe function f:N→N (N is the set of natural numbers defined by f(n)=2n+3 is :
View Solution
